Matter and Radiation
Inside the Atom
All atoms contain:
- A positively charged nucleus composed of protons and neutrons
- Electrons surrounding the nucleus
More information about these particles are below:
Proton
Charge: $+1.60 \times 10^{-19}\,C $
Relative charge: 1
Mass: $1.67 \times 10^{-27}\,kg $Neutron
Charge: $0$
Relative charge: 0
Mass: $1.67 \times 10^{-27}\,kg $Electron
Charge: $-1.60 \times 10^{-19}\,C $
Relative charge: -1
Mass: $9.11 \times 10^{-31}\,kg $
Isotopes
Atoms with the same number of protons but different number of neutrons.
The nucleon number is the number of nucleons in a nucleus while the atomic number is the number of protons. These units are used for organising the elements on the periodic table.
Specific Charge
The specific charge of a charged particle is defined as its charge divided by its mass. For example:
Worked Example
A nucleus of Helium has a charge of $+1.60 \times 10^{-19}\,C $ and a mass of $1.67 \times 10^{-27}\,kg $.
$$ \eqalign{
\text{Specific charge} &= \frac {charge}{mass} \\
&= \frac {1.60 \times 10^{-19}}{1.67 \times 10^{-27}} \\
&= 9.58 \times 10^{7}\,Ckg^{-1}}$$
Stable and Unstable Nuclei
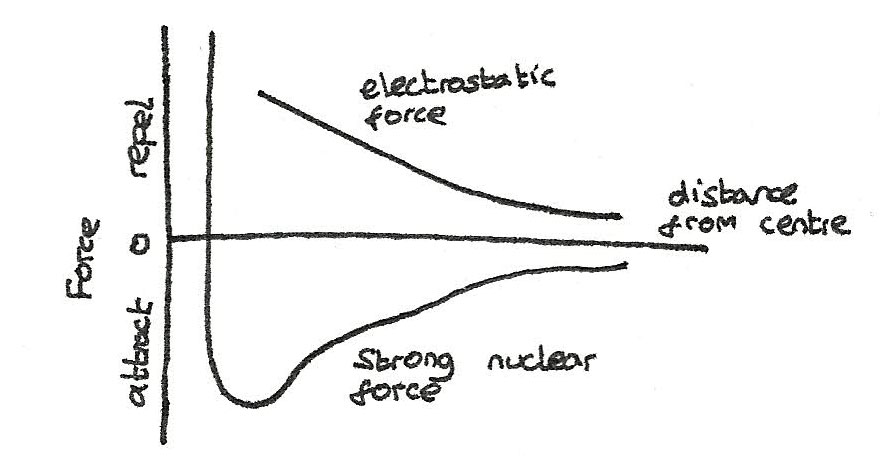
A stable isotope has nucleons that do not disintegrate, as there is the strong nuclear force. This overcomes the electrostatic repulsion between the nucleus and the protons. For the strong nuclear force:
- It's range is no more than 3-4 femtometres (1fm = $10^{-15}m$).
- It has the same effect between protons and neutrons.
- From 3-4 femtometres to around 0.5fm it is an attractive force. Below this it becomes repulsive to prevent neutrons and protons being pushed into each other.
Radioactive Decay
Naturally occurring isotopes release three types of radiation:
- Alpha radiation consists of alpha particles each made of two protons and two neutrons. The equation for alpha decay is shown below:
$$ ^{A}_{Z}X \rightarrow\,^{A-4}_{Z-2}Y +\,^{4}_{2}\alpha $$
- Beta radiation consists of fast moving electrons. The symbol for an electron as a beta particle is $^{~~0}_{-1}\beta$. In beta decay, a beta particle is emitted when a neutron turns into a proton. In addition, an antineutrino ($\overline{\nu}$) is released. The equation is shown below:
$$ ^{A}_{Z}X \rightarrow\,^{~~~~A}_{Z+1}Y +\,^{~~0}_{-1}\beta + \overline{\nu} $$
- Gamma radiation (symbol $\gamma$) is electromagnetic radiation emitted by an unstable nucleus. Gamma radiation is made up of waves, able to passes through metal plates without any mass or charge.
Photons
Visible light is a small part of the electromagnetic spectrum, which is made up of many types of waves of different wavelengths.
| Type | Wavelength | Type | Wavelength |
|---|---|---|---|
| Radio | > 0.1m | Ultraviolet | 400nm- 1nm |
| Microwave | 0.1m - 1mm | X-rays | < 1nm |
| Infrared | 1mm - 700nm | Gamma rays | < 1nm |
| Visible | 700nm- 400nm |
To calculate the frequency or wavelength of a wave, the following equation can be used, where $\lambda$ is the wavelength, $f$ is the frequency and $c$ is the speed of light ($3 \times 10^{8}\,ms^{-1}$):
$$ \lambda = \frac {c}{f} $$
When electromagnetic waves are emitted from beta decay, they are emitted as small bursts of energy known as photons. The energy of a photon can be calculated by:
$$ \text{photon energy E} = hf $$
where $E$ is the energy, $f$ is the frequency and $h$ is a constant referred to as the Planck constant ($6.63 \times 10^{-34}\,J$).
Antiparticles
Antimatter
All particles have a corresponding antiparticle. These are particles that share the exact the same properties as the matter particle except for the charge and the spin. For example an antiproton is a negatively charged particle with the same mass as the proton.
| Particle | Charge | Antiparticle | Charge |
|---|---|---|---|
| proton ($p$) | +1 | antiproton ($\overline{p}$) | -1 |
| neutron ($n$) | 0 | antineutron ($\overline{n}$) | 0 |
| electron ($e$) | -1 | positron ($e^{+}$) | +1 |
| electron-neutrino ($\nu_{e}$) | 0 | electron-antineutrino ($\overline\nu_{e}$) | 0 |
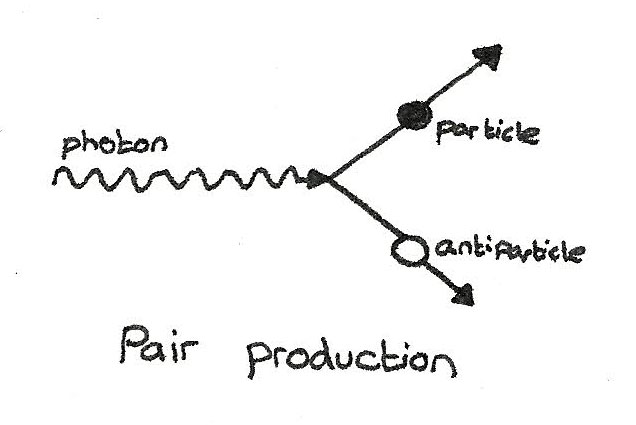
Pair production and Annihilation
When energy is converted into mass, equal amounts of matter and antimatter are produced. This is process is called pair production. If one gamma ray photon passes close by a nucleus, a particle and corresponding antiparticle can be produced.
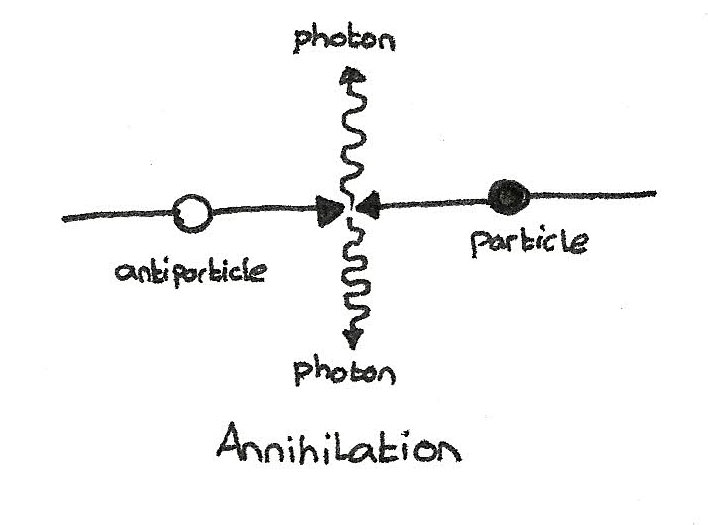
The opposite process is where a particle and its corresponding antiparticle collide, converting the mass back into energy.
Classification of Particles
Particles can be divided into certain groups deepening on their properties.
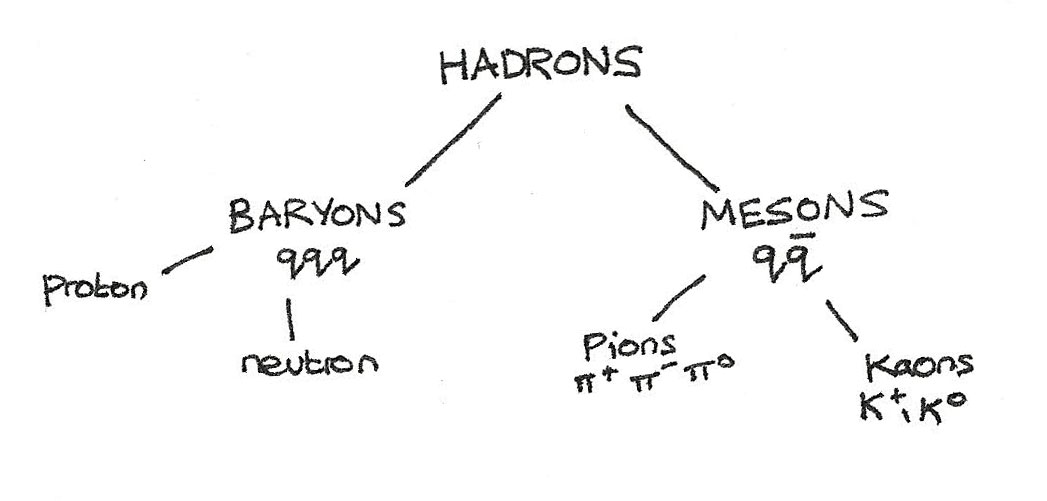
Hadrons
Hadrons are particles that experience the strong nuclear force and are composed of smaller particles called quarks. Hadrons are subdivided into two groups:
Baryons are hadrons that have a $qqq$ quark composition, such as neutrons and protons. All baryons excepts protons decay into protons.
Mesons are hadrons that have a $q\overline{q}$ quark composition. All mesons are unstable and are able to interact with the baryons through the strong interaction.
Leptons
Leptons are fundamental particles that don't feel the strong nuclear force. Examples of leptons include the stable electron ($e^{-}$) and unstable muon ($\mu^{-}$) and tau ($\tau^{-}$) which both decay into electrons.
Neutrinos are also leptons, with a different neutrino for electrons ($\nu_{e}$), muons ($\nu_{\mu}$) and tau leptons ($\nu_{\tau}$). Neutrinos have negligible mass, no charge and only interact through the weak interaction.
Quarks
Quarks are fundamental particles which when arranged together, form hadrons. Three types of quarks, up ($u$), down ($d$) and strange ($s$) have different properties that give the hadrons certain properties. Strange quarks have a property called strangeness.
| Name | Symbol | Charge | Baryon Number | Strangenss |
|---|---|---|---|---|
| up | $u$ | $+\frac{2}{3}$ | $+\frac{1}{3}$ | 0 |
| down | $d$ | $-\frac{1}{3}$ | $+\frac{1}{3}$ | 0 |
| strange | $s$ | $-\frac{1}{3}$ | $+\frac{1}{3}$ | -1 |
| Name | Symbol | Charge | Baryon Number | Strangenss |
|---|---|---|---|---|
| anti-up | $\overline{u}$ | $-\frac{2}{3}$ | $-\frac{1}{3}$ | 0 |
| anti-down | $\overline{d}$ | $+\frac{1}{3}$ | $-\frac{1}{3}$ | 0 |
| anti-strange | $\overline{s}$ | $+\frac{1}{3}$ | $-\frac{1}{3}$ | +1 |
Quark Composition of Baryons
Baryons are composed of three quarks.
Protons have a $uud$ quark combination. This combination gives them a +1 charge and +1 baryon number.
$$ \eqalign {
\text{charge} &= \frac{2}{3} + \frac{2}{3} - \frac{1}{3} = 1 \\
\text{baryon number} &= \frac{1}{3} + \frac{1}{3} + \frac{1}{3} = 1
} $$Neutrons have a $udd$ quark combination. This combination is gives them a 0 charge and +1 baryon number.
$$ \eqalign {
\text{charge} &= \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = 0 \\
\text{baryon number} &= \frac{1}{3} + \frac{1}{3} + \frac{1}{3} = 1
} $$
Antiprotons are $\overline{u}\overline{u}\overline{d}$ and antineutrons are $\overline{u}\overline{d}\overline{d}$.
Quark Composition of Mesons
Mesons are made up of a quark and an antiquark. As $K$ mesons have strangeness, they include a $s$ meson.
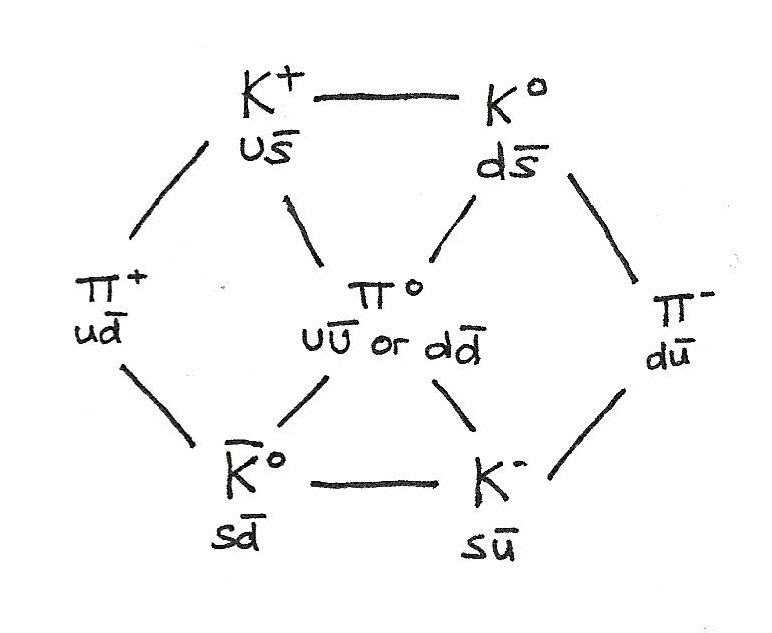
Conservation Laws
When interactions occur, certain laws must be obeyed:
- Charge must always be conserved. In any particle interaction, the total charge after an interaction must equal the the total charge before an interaction.
- Baryon number must always be conserved. The baryon number is the numbers of baryons involved in the interaction. The number of baryons before an interaction must equal the number of baryons after an interaction.
- For strong interactions, strangeness is always conserved. However with the weak interaction, strangeness is not conserved.
- Lepton number must also be conserved. This means that the three individual lepton numbers: $L_{e}$, $L_{\mu}$, and $L_{\tau}$ must individually be conserved.
Exchange Particles
For an interaction to occur, an exchange particle called a gauge boson must be exchanged between particles. There are four fundamental forces, each with its own gauge boson.
| Interaction | Gauge Boson | Particles Affected |
|---|---|---|
| strong | gluon | hadrons |
| electromagnetic | photon | charged particles |
| weak | $W^{+}$, $W^{-}$, $Z^{0}$ | all |
| gravity | graviton | all |
The larger the mass of the gauge boson, the shorter the range of the force. The $W$ boson involved in the weak interaction has a mass 100 times that of a photon meaning it only has a very small range. A photon on the other hand has a zero mass, therefore has an infinite range.
Feynman Diagrams
Feynman diagrams can be used to show interactions. On these diagrams:
- Gauge bosons are shown by the wiggly lines
- Other particles are shown by straight lines
Some interactions are shown below:
Beta Decay

In beta decay, an up quark changes into a down quark which changes a proton into a neutron, or a down quark changes into a up quark, turning a neutron into a proton. An antineutrino is formed in $\beta^{-}$ decay and a neutrino in $\beta^{+}$ decay in order to conserve the lepton number.
$$ n \rightarrow p + e^{-} + \overline{\nu}_{e} \\
p \rightarrow n + e^{+} + \nu_{e} $$
Electron Capture
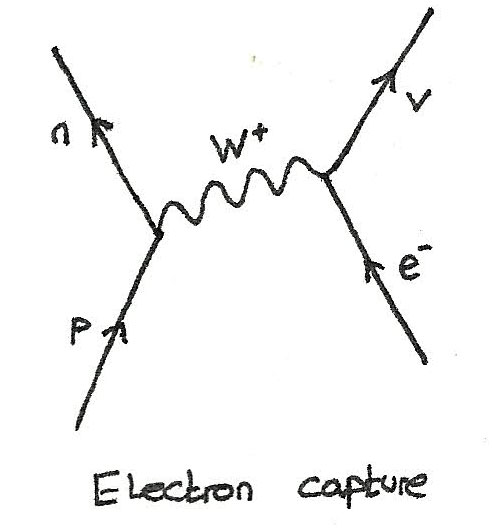
In electron capture, an inner shell electron interacts with a proton from the nucleus.
$$ p + e^{-} \rightarrow n + \nu_{e} $$
Neutrino-Baryon Interaction
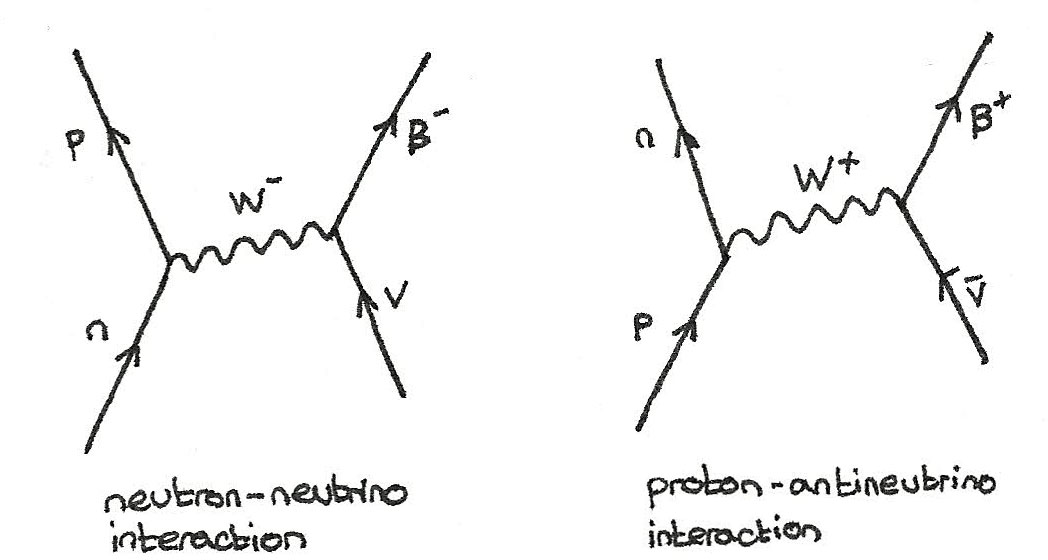
In the interaction between neutrinos and baryons, the baryon changes and an electron or positron is released.
$$ n + \nu_{e} \rightarrow p + e^{-} \\
p + \overline{\nu}_{e} \rightarrow n + e^{+} $$