Radioactivity
Rutherford’s Scattering Experiment
Ernest Rutherford conducted an experiment where a narrow beam of alpha particles were directed towards a thin gold foil. The apparatus he used is shown below.
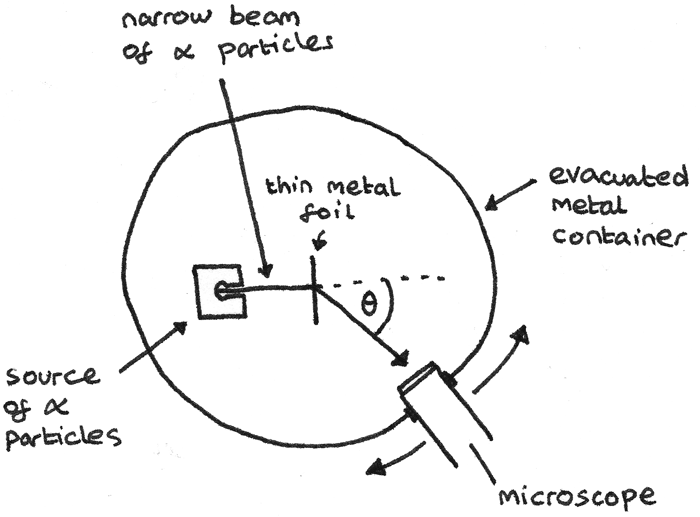
In this apparatus:
- The chamber is evacuated to ensure that the air particles do not interact with the $\alpha$ particles.
- The foil is thin in order to minimise the chance of the $\alpha$ particles been deflected multiple times.
- All of the incident charged particles must have the same kinetic energy otherwise slower particles would be deflected more.
From this experiment he made some observations:
- Although most $\alpha$ particles passed straight through, around 1 in 2000 $\alpha$ particles were deflected by the foil.
- Around 1 in 10000 $\alpha$ particles were deflected backwards through angles greater than 90°.
From these observations, Rutherford interpreted that:
- Most of an atom’s mass is concentrated in the centre of an atom, in the nucleus. This was shown by how most alpha particles could pass through without deflection.
- As the positively charged $\alpha$ particles are repelled, this shows that the nuclei are positively charged.
Types of Radiation
Rutherford conducted more experiments to determine the type of radiation emitted when a nucleus decays. Three types of radiation were found to be commonly emitted:
- $\alpha$ radiation: Every alpha particle consists of two protons and two neutrons, which is the same as a helium nucleus. The two protons give alpha particles a $2+$ charge.
- $\beta$ radiation: Beta radiation consists of fast moving electrons. This gives $\beta$ particles a $1-$ charge.
- $\gamma$ radiation: Unlike alpha and beta particles which are particles, $\gamma$ radiation consists of high frequency photons.
The table below gives a comparison of the three types of radiation:
| $\alpha$ | $\beta$ | $\gamma$ | ||
|---|---|---|---|---|
| Description | 2 protons and 2 neutrons | $\beta^{-}$ is an electron. $\beta^{+}$ is an positron. | High frequency photons | |
| Range in air | <10cm | <1m | Follows inverse square law | |
| Deflection in magnetic field | Easily deflected | Opposite direction to $\alpha$ and less easily | Not deflected | |
| Absorption | Stopped by paper | Stopped by thin sheet of aluminium | Reduced by several centimetres of lead | |
| Ionisation | Intense, produces $10^4$ ions per mm | Less intense, produces about 100 ions per mm | Weak ionising effect |
Absorption Tests
The range of different types of radiation can be determined using a Geiger tube and a counter. A Geiger–Müller tube is an instrument used for the detection of ionised particles. The count rate is the number of ionised particles detected by the tube per unit time. The apparatus is shown below:
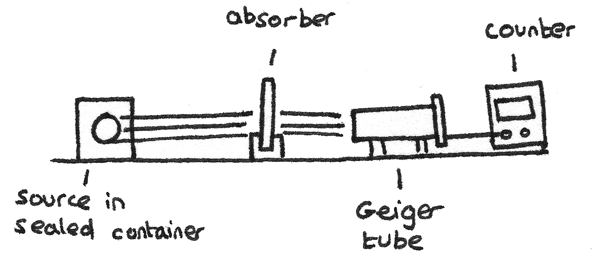
- In using this apparatus, first the background radiation should be measured with the radioactive source out of range of the detector.
- The count rate can then be measured with the source a fixed distance away from the tube. This distance depends on the type of radiation used. A corrected count rate can be calculated by subtracting the background radiation measurement from this value.
- Absorbers of different thickness and materials can be placed between the detector and the source with the corrected count rate measured each time. By comparing the effects of the absorbers on the count rate, the type of radiation emitted by the source can be determined.
Inverse Square Law
By measuring the corrected count rate at varying distances from a $\gamma$ source in air, the inverse square law can be observed. The inverse square law states:
$$ I = \frac{k}{x^{2}} $$
Where $I$ is the relative intensity of the source at distance $x$ from the source and $k$ is a constant. This means that if the source is moved twice the distance away from the detector, the count rate is reduced to a quarter of its original value.
Background Radiation
In our everyday lives we are exposed to low levels of radiation which contribute to an overall dose of background radiation. Some contributors include:
- Air: Radioactive isotopes exist in the air such as radon gas and thorium gas.
- Cosmic Rays: High energy particles and gamma rays bombard the Earth from space.
- Medical Uses: Procedures such as X-rays and cancer treatments often make use of radioactive sources.
Other sources of background radiation include rocks such as granite which contain radioactive isotopes, intake through food and drink and industrial uses. Man-made sources only contribute a small proportion of radiation to the total background radiation count.
Radioactive Decay
When a radioactive isotope decays, the mass of the isotope often changes as a radioactive particle is emitted.
Half Life
The half life of a radioactive isotope is the time taken for the mass of the isotope to decrease to half of its original mass.
The mass of a radioactive isotope with a constant half life decreases exponentially. As radioactive decay is a random process, the number of nuclei that decay are proportional to the number of nuclei remaining.
Activity
The activity, $A$, of a radioactive isotope is the number of nuclei that disintegrate per second. It is measured in becquerels ($Bq$). The rate of change of the number of nuclei per second can be represented by the equation:
$$ \frac{\Delta N}{\Delta t} = -\lambda N $$
Where $N$ is the number of radioactive nuclei and $\lambda$ is the decay constant ($s^{-1}$). As activity is the rate of decay of a radioactive isotope, it follows that:
$$ A = \lambda N $$
Decay Constant
The decay constant $\lambda$, is the probability of an individual nucleus decaying per second. The decay constant is related to the half life of an isotope by the equation:
$$ T_{\frac{1}{2}} = \frac{\ln 2}{\lambda} $$
This means that an isotope with a small decay constant has a smaller probability of decaying per second therefore a longer half life.
Exponential Decay
As the mass of radioactive isotope decays exponentially, it can be represented by an exponentially decreasing graph.
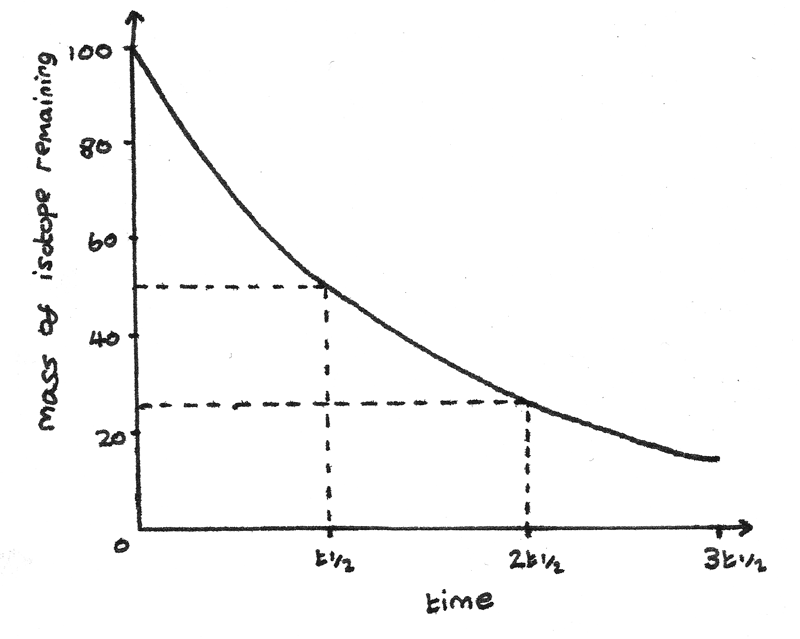
This graph has this equation:
$$ N = N_{0}e^{-\lambda t} $$
Where $N_{0}$ is the initial number of nuclei, $\lambda$ is the decay constant and $t$ is the time in seconds since the decay started.
By substituting in the formula for activity it can also be shown that:
$$ A = A_{0}e^{-\lambda t} $$
Uses of Radioactive Isotopes
Radioactive isotopes have many uses in everyday applications, some of which are described below.
Carbon Dating
The radioactivity of carbon-14 is used to date organic materials. $_{ 6 }^{ 14 }{ C }$ is formed in the upper atmosphere by cosmic rays knocking out neutrons from nuclei which then interact with nitrogen atoms.
$$ _{ 0 }^{ 1 }{ n } ~ + ~ _{ 7 }^{ 14 }{ N } ~ \rightarrow ~_{ 6 }^{ 14 }{ C } ~ + ~ _{ 1 }^{ 1 }{ p } $$
During the life of a plant, the plant continuously takes in carbon-14 and maintains a constant level. Once the plant dies, carbon-14 is no longer taken in and the built up levels start to decay. As the half life of carbon-14 is known, it is possible to determine the age of an organic material by comparing the number of nuclei in a living and a dead sample.
Worked Example
A piece of wood taken from an axe handle found on an archaeological site has $0.375$ times as many carbon-14 atoms as an equal mass of living wood. The half life of carbon-14 is $5740$ years. Calculate the age of the axe handle.
The first step is to calculate the radioactive decay constant ($ \lambda$) for carbon-14.
$$ \eqalign{ T_{\frac{1}{2}} &= \frac{\ln 2}{\lambda} \\
\lambda &= \frac{\ln 2}{T_{\frac{1}{2}}} \\
\lambda &= \frac{\ln 2}{5740} \\
\lambda &= 1.2 \times 10^{-4}~\text{yr}^{-1}} $$Now the age of the axe handle can be calculated by comparing the number of carbon-14 atoms in the handle to the equal mass of living wood.
$$ \eqalign{ N &= N_{0}e^{-\lambda t} \\
(0.375)~N_{0} &= N_{0}e^{-\lambda t} \\
0.375 &= N_{0}e^{-1.2 \times 10^{-4} t} \\
-1.2 \times 10^{-4} t &= \ln 0.375 \\
t &= 8170 \text{ years}}$$
Radioactive Tracers
Radioactive isotopes can be injected into pipelines or even the human body. A radiation detector can then be used on the surface to determine the path the radioactive isotope takes. The isotope technetium-99m is often used in medical diagnosis. The isotope used:
- Must be $\gamma$ or $\beta$ so it can be detected from the surface.
- Should have a half life long enough to last for the duration of the measurements but not too long that its disposal or storage is difficult.
Nuclear Stability
A nucleus is under the influence of the attractive strong nuclear force acting on all nucleons and the repulsive electrostatic force acting between protons. The ratio of protons to neutrons in a nucleus is important in determining the stability of a compound.
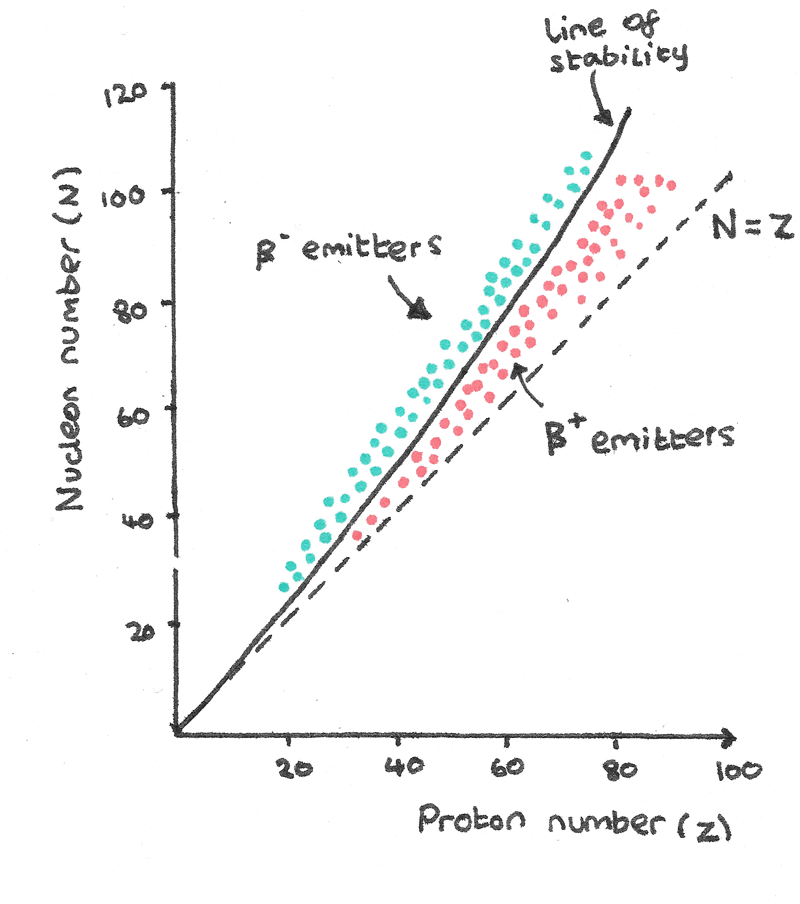
- Stable isotopes with a proton number less than 20 follow the $N = Z$ line, where the isotopes have equal numbers of protons and neutrons.
- Above $Z = 20$, the stable nuclei have more neutrons than protons. The added neutrons bind the protons together with the strong nuclear force which are being repelled by the electrostatic force.
Alpha emission in heavy nuclei
In very heavy nuclei containing more than 82 protons, an alpha particle can be emitted, decreasing the proton number by two and nucleon number by four.
$$ _{ 92 }^{ 238 }{ U }~ \rightarrow ~ _{ 90 }^{ 234 }{ Th } ~ + ~ _{ 2 }^{ 4 }{ \alpha } $$
In alpha emission, all the particles from a given source have the same kinetic energy as the nucleus and the $\alpha$ particles move apart with equal and opposite momentum.
Beta-minus emission in neutron rich nuclei
In neutron rich nuclei above the stability curve, $\beta^{-}$ decay occurs. Beta-minus decay occurs when a neutron decays to produce a proton, electron and antineutrino. The proton remains in the nucleus while the electron and antineutrino are emitted.
$$ _{ 75 }^{ 188 }{ Re }~\rightarrow~ _{ 76 }^{ 188 }{ Os } ~+~ _{ -1 }^{ 0 }{ \beta^{-} } ~+~ { \overline{\nu}_e} $$
Beta-plus emission in neutron rich nuclei
In proton-rich nuclei, below the stability curve, $\beta^{+}$ decay occurs. Beta-plus decay occurs when a proton decays to produce a neutron, positron and neutrino. The neutron remains in the nucleus while the positron and neutrino are emitted.
$$ _{ 12 }^{ 23 }{ Mg }~\rightarrow~ _{ 11 }^{ 23 }{ Na } ~+~ _{ +1 }^{ 0 }{ \beta^{+} } ~+~ { \nu_{e}} $$
Gamma Emission
After emitting an $\alpha$ or $\beta$ particle, the daughter nucleus may be in an excited state and have excess energy. In de-exciting from an excited state to the ground state, $\gamma$ photons are released with energy equal to the difference in energy levels.
Radioactive Series
Unstable nuclei often decay to form a different radioactive isotope. This can result in a series of unstable nuclei before a stable isotope is formed. For example, the uranium isotope $_{ 92 }^{ 238 }{ U }$ has a half life of 4500 million years and decays through a series outlined below:
$$ _{ 92 }^{ 238 }{ U } \overset{\alpha}{\rightarrow}~
_{ 90 }^{ 234 }{ Th } \overset{\alpha}{\rightarrow}~
_{ 88 }^{ 230 }{ Ra } \overset{\beta^{-}}{\rightarrow}~
_{ 89 }^{ 230 }{ Ac } \overset{\beta^{-}}{\rightarrow}~
_{ 90 }^{ 230 }{ Th } \overset{\alpha}{\rightarrow}~
_{ 88 }^{ 226 }{ Ra } \rightarrow~\dots~\rightarrow~
_{ 82 }^{ 206 }{ Pb }$$
Nuclear Radius
Several techniques can be used to find an approximation for the radius of a nucleus.
Closest Approach of $\alpha$ Particles
When an $\alpha$ particle is fired at a gold nucleus and is repelled back through an angle of exactly $180°$, there is a point where the $\alpha$ particle would have stopped a short distance from the nucleus. Due to the conservation of energy, assuming no energy loss, the electrostatic potential energy will be equal to its initial kinetic energy.
$$ \text{Initial } E_{k} = E_{p} = \frac{Qq}{4\pi \epsilon_{0}r} $$
Where $Q$ is the charge of the gold nucleus, $q$ is the charge of the $\alpha$ particle, $\epsilon_{0}$ is the permittivity of free space ($8.85 \times 10^{-12}~Fm^{-1}$) and $r$ is the distance between the nucleus and the centre of the $\alpha$ particle.
Electron Scattering
When a thin beam of high energy electrons is directed towards a thin metal foil, the electrons are diffracted by the nuclei of the metal. This diffraction occurs because the de Broglie wavelength of the electrons is similar to the diameter of the nuclei. A detector can be used to measure the intensity of electrons at different angles from the zero-order.
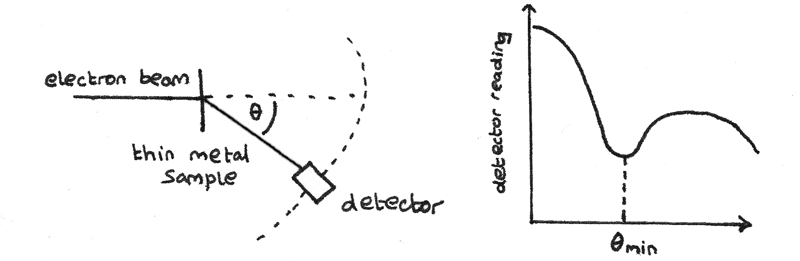
Diffraction of the electrons results in maxima and minima to be superimposed. The angle of the first minimum $\theta_{min}$ is measured and can be used to determine the radius of a nucleus. The de Broglie wavelength of an electron can be calculated using:
$$ \lambda = \frac{hc}{E} $$
Where $\lambda$ is the de Broglie wavelength, $h$ is Plank's constant ($6.63 \times 10^{34}~Js$), $c$ is the speed of light ($3.00 \times 10^{8}~ms^{-1}$) and $E$ is the energy of the electrons ($J$). The radius of the nucleus can then be calculated using:
$$ R = {\frac{0.61}\lambda}{\sin \theta_{min}} $$
Advantage of Electron Scattering
Electron scattering and alpha scattering are both techniques to determine the radius of a nucleus. Electron scattering is regarded as a more accurate method for a number of reasons:
- Electrons are point charges unlike $\alpha$ particles which have a sizeable diameter. This adds more complexity to calculations.
- Alpha particles also interact through the strong nuclear force whereas electrons only interact through the electromagnetic force.
- Electrons can be more easily produced and accelerated to a desired velocity using an electron gun.
Nuclear Radius and Nucleon Number
By finding the nuclear radius of nuclei with varying nucleon numbers, a graph of the nuclear radius $R$ against the nucleon number $A$ can be plotted.
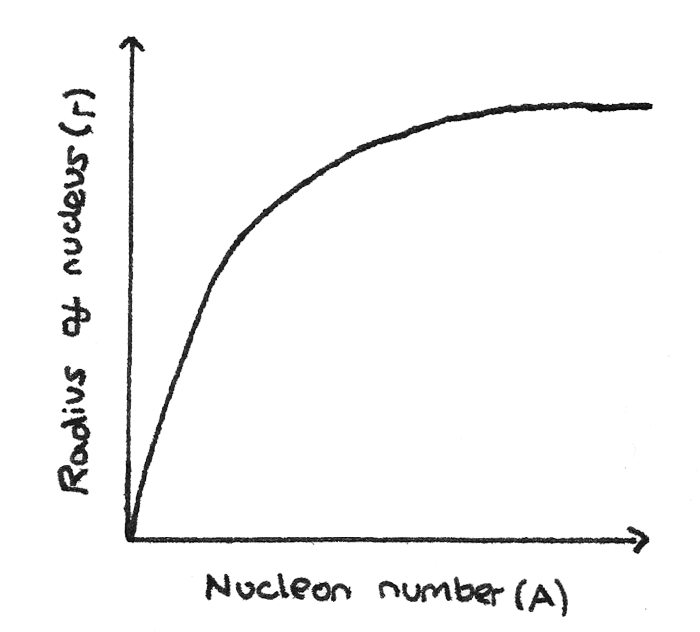
From this graph, the relationship between the mass number and the nuclear radius can be determined:
$$ R = r_{0}A^{\frac{1}{3}} $$
Where $r_{0}$ is the constant $1.05~fm$. Other graphs can be plotted to verify this relationship and give an accurate value of $r_{0}$.
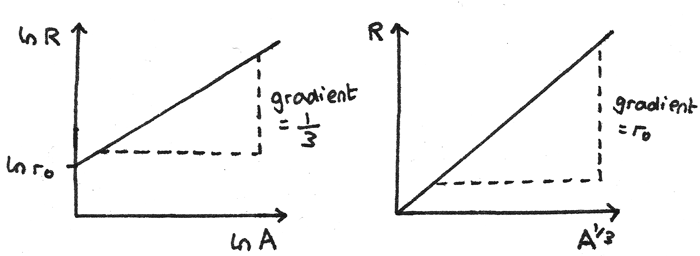
- A graph of $\ln R$ against $\ln A$ gives a straight line graph with y-intercept $\ln r_{0}$ and a gradient of $\frac{1}{3}$.
- A graph of $R$ against $A^{\frac{1}{3}}$ gives a straight line through the origin with a gradient equal to $r_{0}$.
Nuclear Density
As every nucleon has approximately the same mass and volume, all nuclei also have a similar density ($\rho$). By assuming a nucleus is spherical:
$$ V = \frac{4}{3}\pi R^{3} = \frac{4}{3}\pi(r_{0}A^{\frac{1}{3}})^{3} = \frac{4}{3}\pi r_{0}^{3}A $$
This shows that the volume of a nucleus is proportional to its nucleon number and its mass. This shows that the density is constant for all nuclei, and throughout a nucleus.
Worked Example
Calculate the density of a carbon-12 nucleus.
- First the mass can be calculated using the atomic mass unit, ($u = 1.661 \times 10^{-27}~kg$).
$$ \eqalign{ m &= (1.661 \times 10^{-27}) \times 12 \\
&= 1.99 \times 10^{-26}~kg } $$ - The volume can be calculated using:
$$ \eqalign{ V &= \frac{4}{3}\pi r_{0}^{3}A \\
&= \frac{4}{3}\pi(1.05 \times 10^{-15})^{3}(12) \\
&= 5.82 \times 10^{-44}~m^{3}} $$ - The density can now be calculated:
$$ \rho = \frac{m}{v} = \frac{1.99 \times 10^{-26}}{5.82 \times 10^{-44}} = 3.42 \times 10^{17}~kgm^{-3} $$
Repeating this for other elements would give the same nuclear density.
As the nuclear density is so large, a cubic millimetre of nuclear matter would have a mass of around 340 million kilograms. This shows that the majority of an atom must be empty space.