Nuclear Energy
Energy and Mass
Albert Einstein's famous equation shows the relationship between mass and energy:
$$ E = mc^{2} $$
Where $E$ is the energy, $m$ is the mass and $c$ is the speed of light in free space. Reactions on a nuclear and sub-nuclear scale often involve changes in mass, therefore changes in energy. When a nucleus splits into its constituent nucleons, energy is released.
Binding Energy
The binding energy is the work that must be done in order to separate a nucleus into its constituent neutrons and protons.
Mass Defect
The mass defect of a nucleus is the difference between the total mass of the separated nucleons and the mass of the combined nucleus. This mass defect is shown in radioactive decays:
Worked Example
Calculate the binding energy per nucleon of $_{26}^{56}{Fe}$ in $MeV$.
Mass of $ _{26}^{56}{Fe}$ atom = $55.93493~u$
Mass of proton = $1.00728~u$
Mass of neutron = $1.00867~u$
Mass of electron = $0.00055~u$
First the mass of the atom without the electrons and the total sum of the nucleons need to be calculated.
$$ \eqalign{ \text{mass of } _{26}^{56}{Fe} \text{ nucleus} &= 55.93493 - (26 \times 0.00055) \\
&= 55.92063~u} \\ \eqalign{ \text{mass of nucleons} &= (26 \times 1.00728) + (30 \times 1.00867) \\
&= 56.44938~u} \\
\eqalign{ \Delta M &= 56.44938 - 55.92063 \\
&= 0.52875~u } $$
Now the mass defect has been calculated, this must converted into binding energy. This can be done using the conversion: $1u = 931.5 MeV$.
$$ \eqalign{ E &= 0.52875 \times 931.5 \\ &= 492.5~MeV } $$
The binding energy needs to be divided by the number of nucleons to determine the binding energy per nucleon.
$$ \text{binding energy / nucleon} = \frac{492.5}{56} = 8.795~MeV $$
Nuclear Stability
The stability of an isotope depends on the binding energy per nucleon. The greater the binding energy per nucleon, the more stable an isotope is. The graph below shows the binding energy per nucleon ($MeV$) against the mass number, $A$.
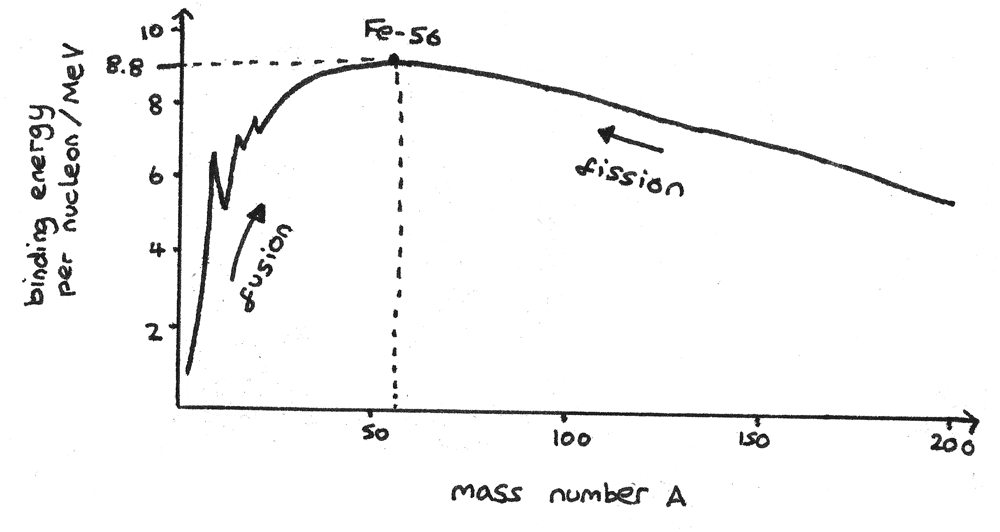
The region around the peak of this graph are the most stable isotopes of iron ($Fe$). Nuclear reactions release energy through increasing the binding energy per nucleon:
- Nucleons with a mass number less than the peak release energy through nuclear fusion. In this process, two light nuclei fuse together to form a larger, more stable nucleus.
- Nucleons with a mass number greater than the peak release energy through nuclear fission. In this process, a large unstable nucleus is split into two lighter, more stable nuclei.
Fusion
Nuclear fusion is the combining of two light nuclei to form a heavier, more stable nucleus. In order to overcome the electrostatic repulsion between two positively charged nuclei and get close enough for the strong force to hold them together, they must be collided at high speed.
An example of a fusion reaction is the fusion of hydrogen isotopes to form helium. This reaction occurs in the Sun, as the high temperatures enable the nuclei to collide at high speeds.
$$ _{1}^{2}{H} ~+~ _{1}^{1}{H} ~\rightarrow~ _{2}^{3}{He} ~+~ \text{energy}$$
Fission
Nuclear fission is the splitting of a heavy unstable nucleus into two lighter, more stable nuclei. This can happen spontaneously in nature, or can be induced through the bombardment of slow moving neutrons. This is called induced fission.
In induced fission, a uranium-235 nucleus ($ _{92}^{235}{U}$) is bombarded with slow moving neutrons, called thermal neutrons. A large nucleus then splits into two approximately equal fragments. Below is an example of a fission reaction:
$$ _{92}^{235}{U} ~+~ _{0}^{1}{n} ~\rightarrow~ _{56}^{144}{Ba} ~+~ _{36}^{90}{Kr} + 2~_{0}^{1}{n} ~+~ \text{energy}$$
As shown in this reaction, further neutrons are released. These neutrons are able to induce fission in other heavy nuclei resulting in a chain reaction.
Nuclear Reactors
A nuclear reactor in a nuclear power station generates electricity through nuclear fission. Enriched uranium fuel rods rich in $_{92}^{235}{U}$ undergo fission reactions in a steady, constant chain reaction. These reactions produce heat which is used to boil water and turn turbines in order to generate electricity.
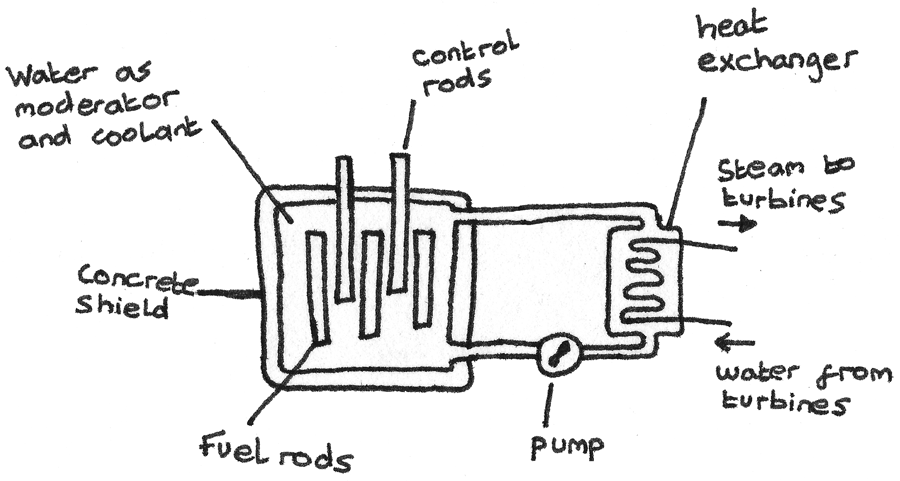
- The nuclear core is encased in thick concrete which acts as shield against the radiation.
- A moderator is used to moderate the speed of the thermal neutrons so they are able to induce fission. Water or graphite is often used.
- Control rods absorb neutrons in the core. By adjusting the height of the rods, the rate of fission reactions in the chamber can be kept constant. In an emergency, the chain reaction can be stopped by dropping the rods. These are often made of boron.
- Coolant is used to remove excess heat produced through the fission.
Waste Products
Waste from nuclear reactors may be highly radioactive and toxic so their handling and disposal require care to minimise danger to the environment and human health. Radioactive waste is categorised according to its nuclear activity.
High level radioactive waste such as spent fuel rods are first stored underwater in cooling pools before being reprocessed or stored securely in sealed containers deep under the oceans. This waste must be stored for centuries as it contains radioactive isotopes with long half lives.
Low level radioactive waste can be sealed in metal containers and buried in large trenches.