Thermal Energy

Temperature Scales

The temperature of an object is a measure of hotness of an object. The hotter an object is, the more internal energy it has. If a warm object is placed in a cold environment, the object loses thermal energy to the surroundings through heat transfer. When the object reaches the same temperature as the environment, they are in thermal equilibrium.

A temperature scale is defined in terms of fixed points:

The Celsius scale of temperature, $°C$ is defined in terms of the ice point, $0°C$, the temperature at which ice melts to water and $100°C$, the temperature at which liquid vaporises to steam.
The absolute scale of temperature in kelvin ($K$) is defined in terms of absolute zero, $0K$ which is the lowest possible temperature and the triple point of water.

Triple Point of Water

The temperature and pressure at which the three phases of water; ice, water and water vapour exist in thermal equilibrium. This is at a temperature of $0.01°C$ and pressure of $0.006~atm$.

Internal Energy

The internal energy of an object is the sum of the random distributions of the kinetic and potential energies of its molecules. Increasing the internal energy of an object through heat transfer increases the kinetic and potential energies associated with the random motion and positions of its molecules.

The internal energy of an object changes if:

Heat transfer or energy transfer through radiation occurs with another object.
Work is done on or by the object.

Specific Heat Capacity

The heat capacity of an object is the energy required to raise its temperature by $1K$. The specific heat capacity of a material is the energy needed to raise the temperature of a $1kg$ mass of an object by $1K$. It is measured in $Jkg^{-1}K^{-1}$.

$$ \Delta Q = mc\Delta T $$

Where $\Delta Q$ is the energy change ($J$), $m$ is the mass ($kg$), $c$ is the specific heat capacity in $Jkg^{-1}K^{-1}$ and $\Delta T$ is the temperature change in kelvin ($K$) or celsius ($C°$).

Inversion Tube Experiment

A method used to determine the specific heat capacity of a substance is the inversion tube experiment. A hollow tube containing lead shot can be inverted multiple times, with the temperature of the lead shot measured after each inversion using a thermometer.

inversion_tube

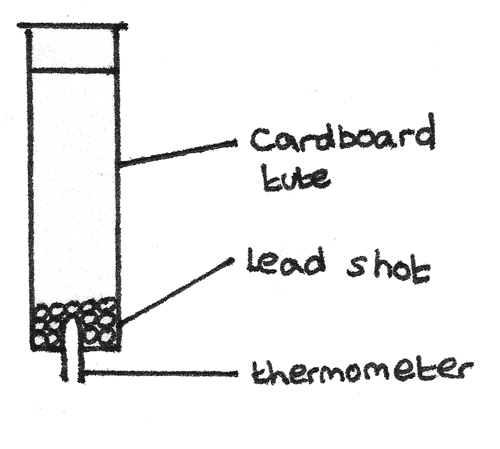
As the tube is inverted and the lead shot switches between the ends of the tube, the temperature rises. This is because the gravitational potential energy is converted into internal energy of the lead shot. Assuming no energy is lost to the surroundings or the tube, the loss in gravitational potential energy is equal to the gain in internal energy.

$$ \eqalign{ mc\Delta T &= mgLn \\
c &= \frac{gLn}{\Delta T}} $$

Where $c$ is the specific heat capacity ($Jkg^{-1}K^{-1}$), $g$ is the acceleration under gravity ($9.81~ms^{-2}$), $L$ is the length of the tube ($m$), $n$ is the number of inversions and $\Delta T$ is the temperature change ($K$).

Calorimeter

A method of determining the specific heat capacity of a liquid is by using a calorimeter and a heater.

calorimeter

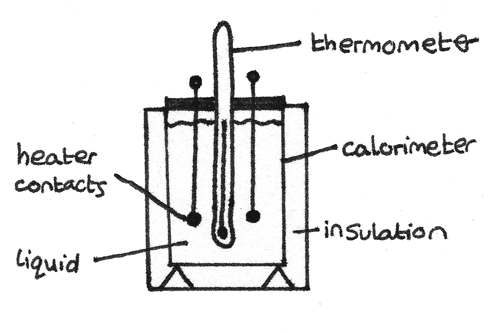
With the heater in the liquid, the liquid should be stirred and the temperature measured over time. As the calorimeter is well insulated, it can be assumed no energy is lost to the surroundings. With a known current and voltage, the energy supplied by the heater can be calculated by:

$$ \text{energy supplied by heater} = IV\Delta t $$

Where $I$ is the current ($A$), $V$ is the voltage ($V$) and $\Delta t$ is the time ($s$) the heater is in the liquid. As some energy is used to heat the liquid and some to heat the calorimeter:

$$ IV\Delta t = m_{1}c_{1}\Delta T + m_{cal}c_{cal}\Delta T $$

Where $m_{1}$ and $m_{cal}$ are the masses of the liquid and the calorimeter and $c_{1}$ and $c_{cal}$ are the specific heat capacities of the liquid and the calorimeter respectively. $\Delta T$ is the temperature change ($K$) measured by the thermometer.

A similar approach can be used to determine the specific heat capacity of a solid whereby a heater is inserted into the solid and the temperature difference is measured over time. These methods depend on a known energy input and the assumption of no energy loss to the surroundings.

Specific Latent Heat

During a phase transition where the state of a substance is changed, energy is required to do work against the attractive forces holding the molecules together. In this process, the energy transferred to the object as heat does not lead to an increase in temperature. The energy required to change the state of a substance with no change in temperature is known as its latent heat, $l$.

The specific latent heat of fusion of a substance is the energy required to change $1kg$ of a solid into $1kg$ of a liquid, with no change in temperature.
The specific latent heat of vaporisation is the energy required to change $1kg$ of a liquid into $1kg$ of a gas, with no change in temperature.

temperature_time

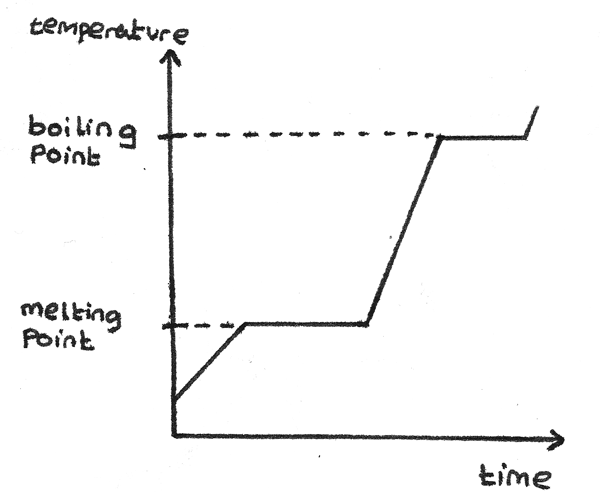
This graph shows the temperature of a solid against the time it is heated for a constant rate. The flat sections of the curve are when the substance is changing state.

The energy, $\Delta Q$ needed to change the state of a substance of mass $m$ can be calculated with:

$$ \Delta Q = ml $$

Where $\Delta Q$ is the energy required ($J$), $m$ is the mass of the liquid ($m$) and $l$ is the specific heat of fusion or vaporisation ($Jkg^{-1}$).