Gas Laws

The molecules of a gas move with varying speeds and with unpredictable motions. This is due to the uneven bombardment from other molecules and the container. This type of random motion is called Brownian motion.

The pressure of a gas is the force per unit area that the gas exerts normally on the surface of a container. It is measured in pascals ($Pa$) where $1~Pa = 1~Nm^{-2}$. The pressure is a result of the high frequency impacts between the individual molecules of a gas and the container. The pressure depends on the temperature, volume and the mass of the gas in the container.

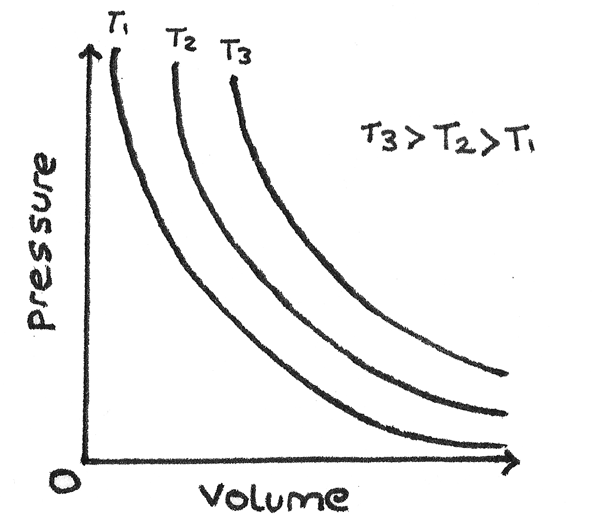
Boyle's Law

Boyle's Law states that for a gas of fixed mass at a constant temperature, the pressure ($p$) and volume ($V$) are inversely proportional:

$$ pV = \text{constant} $$
A change made at constant temperature is known as an isothermal process.

boyles_law

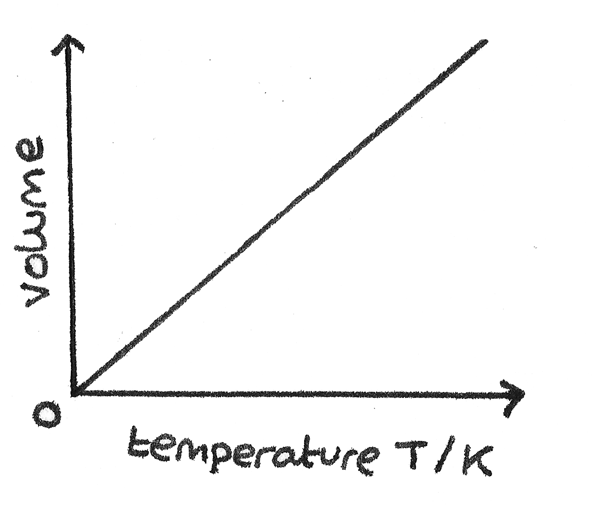
Charles's Law

Charles's Law states that for a gas of fixed mass at constant pressure, the volume, $V$ is directly proportional to its absolute temperature, $T$.
$$ \frac{V}{T} = \text{constant} $$
charles_law

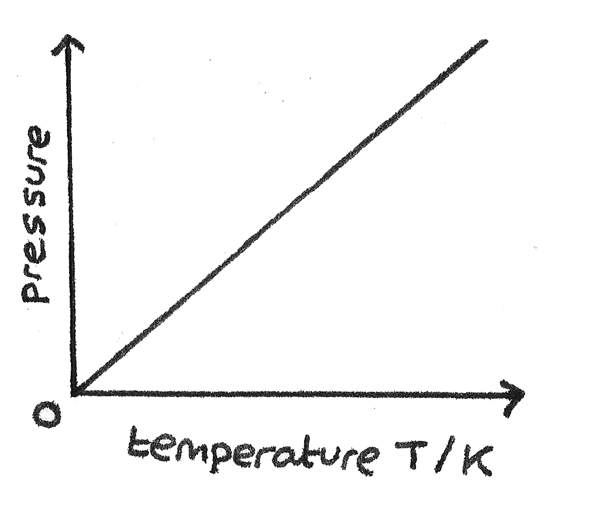
Pressure Law

The pressure law states that for a gas of fixed mass at constant volume, the pressure, $p$ is directly proportional to its absolute temperature, $T$.
$$ \frac{p}{T} = \text{constant} $$
pressure_law

Ideal Gas Equation

In order to determine the ideal gas equation, some definitions relating to the amount of substance must be known:

Mole

One mole is the amount of any substance containing as many particles as there are carbon atoms in exactly $12g$ of carbon-12.

Molar Mass

The molar mass of a substance is the mass ($g$) of 1 mole of the substance. Molar mass and the number of moles are related by the equation:

$$ n = \frac{m}{M} $$

Where $n$ is the number of moles, $m$ is the mass ($g$) and $M$ is the molar mass ($gmol^{-1}$).

Avogadro Constant

The Avogadro constant, $N_{A}$ is defined as the number of atoms in exactly $12g$ of carbon-12. The value of $N_{A}$ is $6.02×10^{23}~mol^{−1}$. One mole of any substance contains $N_{A}$ particles.

Ideal Gas

An ideal gas is a gas that obeys Boyle's Law. The three experimental gas laws can be combined to give the equation:
$$ \frac{pV}{T} = \text{constant} $$
Where $p$ is the pressure ($Pa$), $V$ is the volume ($m^{3}$) and $T$ is the temperature in kelvin ($K$) for a fixed mass of an ideal gas.

The constant in this equation depends on the number of moles of the gas used. By using a constant known as the molar gas constant ($R =~8.31~Jmol^{-1}K^{-1}$), the combined gas law may be written as:

$$ \frac{pV}{T} = nR \\
pV = nRT $$

This equation is known as the ideal gas equation.

The number of particles in a gas is given by the number of moles multiplied by the Avogadro's constant, $N_{A}$:

$$ N = nN_{A} $$

A constant known as Boltzmann's constant, $k= 1.38 \times 10^{-23}~JK^{-1}$, can be considered as the gas constant for one molecule of gas:
$$ k = \frac{R}{N_{A}} $$

By substituting these equations into the ideal gas equation, it can be found that:

$$ pV = NkT $$
Where $p$ is the pressure ($Pa$), $V$ is the volume ($m^{3}$), $T$ is the temperature ($K$), $k$ is the Boltzmann constant ($1.38 \times 10^{-23}~JK^{-1}$) and $N$ is the number of molecules in the gas.

Assumptions of Ideal Gases

To formulate the equations shown above, some assumptions must be made about the molecules and the container:

The gas contains a large number of particles.
The particles move rapidly and randomly around the container in continual motion.
All collisions between the particles and the container are perfectly elastic so kinetic energy is conserved.
The particles follow Newton’s laws of motion.
No attractive forces act between particles.
Any forces that act during collisions are instantaneous.
The molecules are point molecules. This means the total volume of the particles is negligible compared to the volume of the container.

A gas obeying these assumptions is an ideal gas. Under conditions where the ideal gas equation no longer holds, one of these assumptions is no longer valid. For example, in a gas at very high pressure, the molecules are so close to each other that their volume is significant so is no longer an ideal gas.

Kinetic Theory

The gas laws can be explained using kinetic theory which models a gas as point molecules moving about in random motion, continually colliding with the container walls. This gives an explanation for:

Boyle’s Law: The pressure of a gas is increased at constant temperature by reducing the volume as the particles have to travel less distance between collisions with the container walls. This causes more impacts per second, so the pressure is greater.
Pressure Law: The pressure of a gas is increased as the temperature is increased as the average kinetic energy of the particles is greater. This causes the speed of the particles to increase resulting in harder and more frequent collisions with the walls of the container.

Molecular Speeds

The molecules in an ideal gas have a continuous spread of speeds, shown by the graph below. If the temperature is raised, this curve becomes broader and flatter as more molecules have higher speeds.

speed_distribution

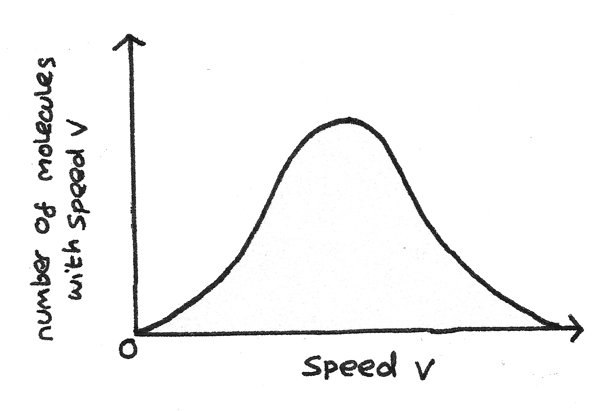
The root mean square speed of the molecules is defined as:
$$ c_{rms} = \sqrt{ \frac{(c_{1}^{~2} + c_{2}^{~2} + \dots + c_{N}^{~2})}{N} }$$
Where $c_{1}$, $c_{2}$ $\dots~c_{N}$ are the speeds of the individual molecules and $N$ is the number of molecules in the gas.

Kinetic Theory Equation

For an ideal gas consisting of $N$ identical molecules, each of mass $m$, in a container of volume $V$ and pressure $p$,
$$ pV = \frac{1}{3}Nmc_{rms}^{~~~~~~2} $$
This formula can be derived using kinetic gas theory along with Newton’s laws of motion.

Derivation of Kinetic Theory Equation

Consider one molecule of mass $m$ in a rectangular box of dimensions $l_{x}$, $l_{y}$ and $l_{z}$. The velocity components of this molecule are represented by $u_{1}$, $v_{1}$ and $w_{1}$ respectively.

particles_container

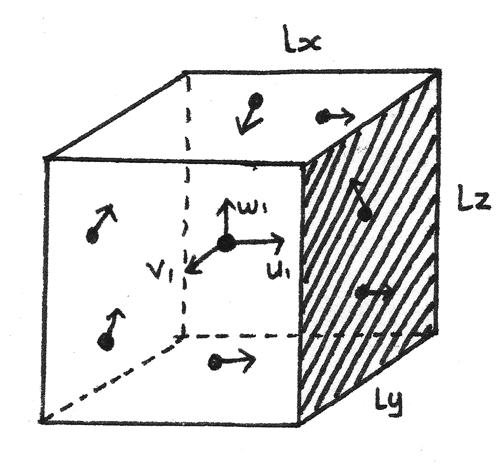
If the molecule impacts the shaded side of the container with velocity $u_{1}$, in a perfectly elastic collision:
$$ \eqalign{ \text{momentum before} &= mu_{1} \\
\text{momentum after} &= -mu_{1} \\
\text{change in momentum} &= -mu_{1} - mu_{1} \\
&= - 2mu_{1}} $$
The time taken between the impacts of the molecule and the shaded side of the container is:
$$ \eqalign{
\text{time} &= \frac{\text{distance}}{\text{average speed}} \\
t &= \frac{2l_{x}}{u_{x}}} $$
Where $2l_{x}$ is twice the width of the container and $u_{x}$ is the horizontal velocity component of the molecule.
Using Newton’s Second Law of motion that the force is equal to the rate of change of momentum:
$$ \eqalign{ Ft &= \Delta(mv) \\
F\frac{2l_{x}}{u_{1}} &= -2mu_{1} \\
F &= \frac{-mu_{1}^{2}}{l_{x}}} $$
By Newton’s third law, the container will also apply an equal and opposite force on the molecule. Therefore the force equals:
$$ F = \frac{mu_{1}^{2}}{l_{x}} $$
As the pressure contributed by this molecule is the force per unit area, where the force has been calculated above and the area of the shaded region is $l_{z}l_{y}$:
$$p_{1} = \frac{F}{A} = \frac{mu_{1}^{2}}{l_{x}l_{z}l_{y}} \\
\text{volume, } V = l_{x}l_{z}l_{y} \\
p_{1} = \frac{mu_{1}^{2}}{V} $$
For $N$ molecules moving in the container, the total pressure is the sum of all the pressures, therefore:
$$ \eqalign{ p &= \frac{mu_{1}^{2}}{V} + \frac{mu_{2}^{2}}{V} + \dots + \frac{mu_{N}^{2}}{V} \\
p &= \frac{m}{V}\big(u_{1}^{2} + u_{2}^{2} + \dots + u_{N}^{2})}$$
Using the root mean square formula for $u_{N}$:
$$ \eqalign{\overline{u^{2}} &= \frac{(u_{1}^{~2} + u_{2}^{~2} + \dots + u_{N}^{~2})}{N} \\
p &= \frac{Nm\overline{u^{2}}}{V}} $$
The other components of the molecule’s motion must also be considered. Using Pythagoras’ theorem, the total velocity of a molecule can be calculated with:
$$c^{2} = u^{2} + v^{2} + w^{2}$$
If all $N$ particles are considered the same:
$$c_{rms}^{~~~~~~2} = \overline{u^{2}} + \overline{v^{2}} + \overline{w^{2}}$$
As all the particles are moving randomly in all dimensions:
$$ \overline{u^{2}} = \overline{v^{2}} = \overline{w^{2}} \\
c_{rms}^{~~~~~~2} = 3\overline{u^{2}} $$
By substituting the above formula into the formula for the pressure, the kinetic theory equation has been derived:
$$ \eqalign{ p &= \frac{Nm\overline{u^{2}}}{V} \\
p &= \frac{Nmc_{rms}^{~~~~~~2}}{3V} \\
pV &= \frac{1}{3}Nmc_{rms}^{~~~~~~2}} $$

Molecules and Kinetic Energy

The mean kinetic energy of a molecule of a gas is equal to the total kinetic energy of all the molecules divided by the total number of molecules.
$$ \eqalign{\overline{E_{k}} &= \frac{(\tfrac{1}{2}mc_{1}^{~2} + \tfrac{1}{2}mc_{2}^{~2} + \dots + \tfrac{1}{2}mc_{N}^{~2})}{N}
\\
\overline{E_{k}} &= \frac{\tfrac{1}{2}m(c_{1}^{~2} + c_{2}^{~2} + \dots + c_{N}^{~2})}{N}
\\
\overline{E_{k}} &= \frac{1}{2}mc_{rms}^{~~~~~~2}
} $$
By using the assumption that the mean kinetic energy of a molecule of an ideal gas is $\frac{3}{2}kT$, where $k$ is the Boltzmann constant ($1.38 \times 10^{-23}~JK^{-1}$) and $T$ is the temperature, the ideal gas equation can be derived from the kinetic theory equation:
$$ \eqalign{ \frac{3}{2}kT &= \frac{1}{2}mc_{rms}^{~~~~~~2} \\
3kT &= mc_{rms}^{~~~~~~2} \\
pV &= \frac{1}{3}Nmc_{rms}^{~~~~~~2} \\
pV &= NkT \\ \\
\text{As } ~ Nk &= \frac{NR}{N_{A}} = nR \\ pV &= nRT
} $$

All gases at the same temperature have the same mean kinetic energy. A lighter gas with the same mean kinetic energy as a heavier gas will have a higher average speed per particle.