Oxidation, Ionisation and Orbitals
Oxidation Numbers
An oxidation number is a measure of the number of electrons an atom uses to bond with atoms of another element. Oxidation numbers are derived from a set of rules:
| Species | Oxidation Number |
|---|---|
| Uncombined elements | 0 |
| Combined oxygen | -2 |
| Combined hydrogen | +1 |
| Combined flourine | -1 |
| Combined group 1 elements | +1 |
| Combined group 2 elements | +2 |
In all simple molecules the overall charge is zero and the sum of the oxidation numbers must equal the overall charge. In sulphur dioxide, $SO_{2}$ for example, there are 2 oxygen atoms, each with an oxidation number of $-2$. In total this is a contribution of $-4$. The oxidation number of the sulphur atom must therefore be $+4$ to balance the oxidation number.
Some elements (e.g. transition elements) form compounds and ions where the element is able to have different oxidation numbers. In such case, the oxidation number is included in the name of the compound as a roman numeral.
| Compound | Oxidation Number |
|---|---|
| Iron(II) chloride ($FeCl_{2}$) | $Fe$: +2 |
| Iron(III) chloride ($FeCl_{3}$) | $Fe$: +3 |
| Copper(I) oxide $Cu_{2}O$ | $Cu$: +1 |
| Copper(II) oxide $CuO$ | $Cu$: +2 |
Ionisation Energy
The energy needed to form positive ions is known as the ionisation energy. Ionisation provides evidence for the arrangement of electrons in shells.
First Ionisation Energy
The first ionisation energy is the amount of energy needed to remove one electron from each atom in one mole of gaseous atoms to form one mole of gaseous 1+ atoms. For example:
$$ Na_{(g)} \rightarrow Na^{+}_{(g)} + e^{-}
\hspace3ex
I.E.\,=\,+496\,kJ\,mol^{-1}
$$
Factors Affecting Ionisation Energy
Electrons are negatively charged and are held in shells by the attraction with the positive nucleus. To form an ion, sufficient energy must be provided to overcome this attraction. Electrons in the outermost shells are removed first since they experience the least nuclear attraction. The nuclear attraction depends on three main factors:
- Atomic radius: The greater the atomic radius, the smaller the effect of the nuclear attraction. The greater the number of electrons, the more shells and greater the radius.
- Nuclear Charge: The greater the nuclear charge, the greater the attractive force therefore increasing the ionisation energy.
- Electron Shielding: This is where inner shells of electrons repel outer shell electrons. The more inner shells there are, the larger the shielding and the smaller the effect of the nuclear attraction on the outer electrons. The more shielding, the lower the ionisation energy.
Successive ionisation energy is the energy to required to remove each electron in turn. For example, the second ionisation energy is the energy required to take an electron from a 1+ ion to form a 2+ ion. Each successive ionisation energy is larger than the previous one, due to the increasing electron to proton ratio.
Electrons in Orbitals
Successive ionisation energies provide evidence for the presence of shells and the number of electrons in each shell. Quantum numbers are used to describe the positioning of electrons in an atom:
- The principal quantum number indicates the shell an electron occupies.
- Each shell has a different principal quantum number.
- The larger the quantum number, the further it is from the nucleus.
- The further from the nucleus, the higher the energy level.
Shell
A shell is a group of atomic orbitals with the same principal quantum number, $n$. Every shell holds a certain number of electrons defined by: $2n^{2}$ where $n$ is the principal quantum number.
Atomic Orbitals
An atomic orbital is a region within an atom that is able to hold up to two electrons, with opposite spins. Every shell is made up of orbitals. There are four types of orbitals:
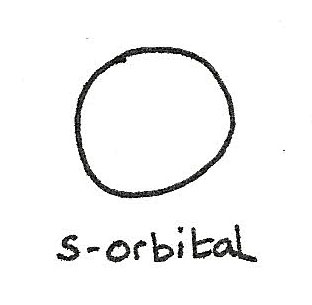
s-orbital
A s-orbital has a spherical shape.
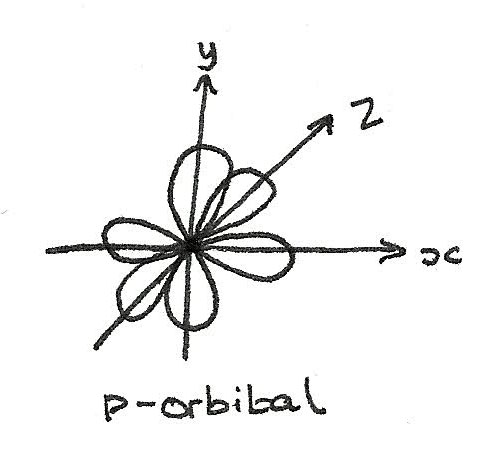
p-orbital
A p-orbital has a 3-dimensional dumbbell shape. From $n=2$, each shell contains three p-orbitals at right angles to each other.
d-orbitals and f-orbitals
The structure of these orbitals are more complex. From $n=3$, each shell contains 5 d-orbitals. From $n=4$, each shell contains 7 f-orbitals.
Orbitals can be represented by boxes, with each box holding up to 2 electrons. The arrows represent the spin of an electron:
$$ \eqalign{
&\text{s-orbital}: \boxed{\uparrow\downarrow} \\
&\text{p-orbital}: \boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow} \\
&\text{d-orbital}: \boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow} \\
&\text{f-orbital}: \boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}\boxed{\uparrow\downarrow}
} $$
Electron Energy Levels
Sub-shells have different energy levels as shown below:
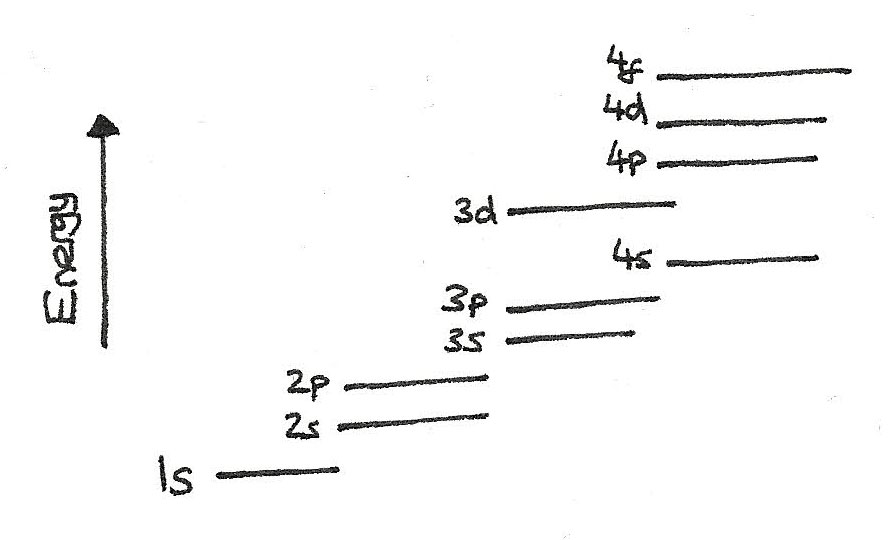
When deciding on the arrangement of electrons in an atom, the Aufbau principle should be followed:
- Electrons are added one at a time to build up an atom.
- The lowest energy levels are filled first.
- Each energy level must be filled before the next level can be filled.
- Each orbital in a subshell is filled singularly before pairing.
- An orbital can hold a maximum of two electrons each with an opposite spin.
An important point when filling up electrons in the subshells is that the $4s$ energy level is below the $3d$ energy level meaning that the $4s$ orbital fills before the $3d$ orbital.
Electron Configuration
To show electron configurations, a shorthand technique can be used. For example for carbon it would be: $1s^{2}\,2s^{2}\,2p^{2}$
This is $nx^{y}$, where $n$ is the shell number, $x$ is the type of orbital and $y$ is the number of electrons in the orbital.
Electrons in the Periodic Table
The periodic table is structured in blocks of 2, 6, 10 and 14 elements linking to the subshells:
- Groups I and II are s-block
- Groups III to VIII are p-block
- Transition elements are d-block
- The f-block is at the bottom of the table.
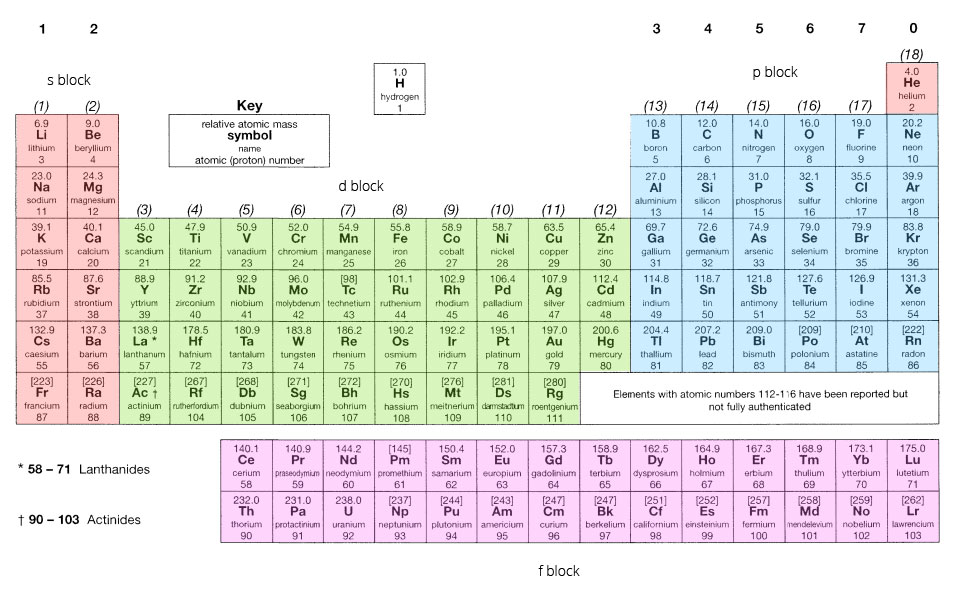
By following the pattern shown above, the electron configuration for any element can be determined using the periodic table.
Shortening an electron configuration
When electron configurations become lengthy, they can be abbreviated using the previous noble gas:
$$ \eqalign{
&K: 1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{6}\,4s^{1} \\
&K: [Ar]\,4s^{1}
}
$$
Electron Configurations of Ions
- When positive ions are formed, electrons are removed from the highest energy orbital.
- When negative ions are formed, electrons are added to the highest energy orbital.
| Element | Electron Configuration |
|---|---|
| $Mg$ | $1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}$ |
| $Mg^{2+}$ | $1s^{2}\,2s^{2}\,2p^{6}$ |
| $Cl$ | $1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{5}$ |
| $Cl^{-}$ | $1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{6}$ |
There is an exception to this rule however. For the elements $Sc$ to $Zn$ at the top of the d-block, the $4s$ subshell is filled before the $3d$ subshell. Once the $4s$ subshell has been filled, it moves to a higher energy level so that when removing electrons, the $4s$ electrons are removed before the $3d$ electrons.
$$ \eqalign{
Fe: &1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{6}\,4s^{2}\,3d^{6} \\
Fe^{2+}: &1s^{2}\,2s^{2}\,2p^{6}\,3s^{2}\,3p^{6}\,\hphantom{4s^{2}}3d^{6}
}
$$