Buffers and Neutralisation

Buffer Solutions

A buffer solution minimises changes in $pH$ when small amounts of an acid or base are added. Buffer solutions can be made from a weak acid and a salt of the weak acid. An example is a mixture of ethanoic acid ($CH_{3}COOH_{(aq)}$) and sodium ethanoate ($CH_{3}COO^{-}Na^{+}_{(aq)}$). In this system:

The weak acid dissociates partially. The position of equilibrium is to the left, so there is a high concentration of the undissociated weak acid.
$$ CH_{3}COOH_{(aq)} \rightleftharpoons H^{+}_{(aq)} + CH_{3}COO^{-}_{(aq)} $$
The salt of the weak acid dissociates completely. This results in a high concentration of the conjugate base $CH_{3}COO^{-}$ in the buffer solution.
$$ CH_{3}COO^{-}Na^{+}_{(aq)} \rightarrow CH_{3}COO^{-}_{(aq)} + Na^{+}_{(aq)} $$

The high concentrations of $CH_{3}COOH_{(aq)}$ and $CH_{3}COO^{-}_{(aq)}$ allow the buffer solution to minimise any changes in the $pH$.

Adding Acid

Upon adding an acid, the $[H^{+}_{(aq)}]$ is increased. The conjugate base ($A^{-}$) reacts with the $H^{+}_{(aq)}$:
$$ A^{-}_{(aq)} + H^{+}_{(aq)} \rightarrow HA_{(aq)} $$

This shifts the position of equilibrium to the left.

Adding Alkali

Upon adding an alkali, the $[OH^{-}_{(aq)}]$ is increased. The small concentration of $H^{+}_{(aq)}$ reacts with the $OH^{-}_{(aq)}$:
$$ H^{+}_{(aq)} + OH^{-}_{(aq)} \rightarrow H_{2}O_{(l)} $$
This shifts the position of equilibrium to the right in order to restore the dissociated $H^{+}$ ions.

$pH$ of Buffer Solutions

For a buffer system, the acid dissociation constant ($K_{a}$) can be calculated as follows:
$$ K_{a} = \frac{[H^{+}][A^{-}]}{[HA]} $$
This formula can be used in order to calculate the $pH$ of the buffer solution. Some key assumptions must be made about a buffer system:

As only a small proportion of $HA$ dissociates, the assumption can be made that the concentration of undissociated $HA_{(aq)}$ is equal to the concentration of $HA_{(aq)}$ at equilibrium.
As the salt of the weak acid dissociates completely, the concentration of the salt of the weak acid is equal to the $[A^{-}]$.

Worked Example

Calculate the $pH$ of a buffer solution at $25°C$ containing $0.07~mol~dm^{-3}$ $ CH_{3}COOH_{(aq)}$ and $0.14~mol~dm^{-3}$ $ CH_{3}COO^{-}Na^{+}_{(aq)}$. For $CH_{3}COOH_{(aq)}$, $K_{a} = 1.9 \times 10^{-5}~mol~dm^{-3}$.

First, the $[H^{+}]$ can be calculated from the acid dissociation constant formula.
$$ \eqalign{[H^{+}_{(aq)}] &= K_{a} \times \frac{[CH_{3}COOH_{(aq)}]}{[CH_{3}COO^{-}_{(aq)}]} \\
[H^{+}_{(aq)}] &= 1.9 \times 10^{-5} \times \frac{0.07}{0.14} \\
[H^{+}_{(aq)}] &= 9.5 \times 10^{-6} ~mol~dm^{-3}
}$$
Now the $pH$ can be calculated:
$$ \eqalign{ pH &= -\log_{10} [H^{+}_{(aq)}] \\
pH &= -\log_{10}(9.5 \times 10^{-6}) \\
pH &= 5.02 } $$

Buffer from a Weak Acid and Strong Base

Buffer solutions can also be formed by reacting an excess of a weak acid with a strong base. In this reaction, some of the weak acid will react with the strong base to form the conjugate base.
$$ CH_{3}COOH + NaOH \rightarrow CH_{3}COO^{-}Na^{+} + H_{2}O $$

Worked Solution

Calculate the $pH$ of the solution formed when $15~cm^{3}$ of $0.1~mol~dm^{-3}$ sodium hydroxide ($NaOH$) is added to $25~cm^{3}$ of $0.2~mol~dm^{-3}$ ethanoic acid ($CH_{3}COOH$). The $K_{a}$ of ethanoic acid is $1.76 \times 10^{-5}~mol~dm^{-3}$.

Moles of the weak acid, $CH_{3}COOH$:
$$ n = cv = (0.2)(25 \times 10^{-3}) = 5 \times 10^{-3}~mol $$
Moles of the base, $NaOH$:
$$ n = cv = (0.1)(15 \times 10^{-3}) = 1.5 \times 10^{-3}~mol $$
As there are less moles of base than moles of weak acid and they react in a $1:1$ ratio, the weak acid must be in excess. The number of moles of ethanoic acid in the buffer solution must then be calculated:
$$ n = 5 \times 10^{-3} - 1.5 \times 10^{-3} = 3.5~\times 10^{-3} mol $$
As the molar ratio between the ethanoic acid and the strong base is $1:1$ , the number of moles of $NaOH$ is equal to the number of moles of $CH_{3}COO^{-}$.

After mixing the acid and the base, the total volume becomes:
$$ 15 \times 10^{-3} + 25 \times 10^{-3} = 40~\times 10^{-3} mol~dm^{-3} $$

This affects the concentrations:
$$[CH_{3}COOH] = \frac{3.5 \times 10^{-3}}{40 \times 10^{-3}} = 8.75 \times 10^{-2} mol~dm^{-3} \\
[CH_{3}COO^{-}] = \frac{1.5 \times 10^{-3}}{40 \times 10^{-3}} = 3.75 \times 10^{-2} mol~dm^{-3} $$

Using the acid dissociation constant equation, the $[H^{+}]$ can be calculated:
$$ \eqalign{ K_{a} &= \frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]} \\
[H^{+}] &= \frac{K_{a} \times [CH_{3}COOH]}{[CH_{3}COO^{-}]} \\
[H^{+}] &= \frac{(1.76 \times 10^{-5})(8.75 \times 10^{-2})}{3.75 \times 10^{-2}} \\
[H^{+}] &= 4.11 \times 10^{-5} mol~dm^{-3}} $$

Now the $pH$ can be calculated using:
$$ \eqalign{ pH &= -log [H^{+}] \\ pH &= -log (4.11 \times 10^{-5}) \\ pH &= 4.39} $$

Buffers in the Body

Healthy human blood plasma requires a $pH$ between $7.35$ and $7.45$. The $pH$ of blood is controlled by a mixture of buffers. Haemoglobin can act as a buffer solution until its buffering capacity is exceeded. The carbonic acid-hydrogencarbonate buffer system is then used.
$$ H_{2}CO_{3 (aq)} \rightleftharpoons H^{+}_{(aq)} + HCO_{3(aq)}^{-} $$

Any increase in $[H^{+}_{(aq)}]$ is removed by the conjugate base, $HCO_{3(aq)}^{-}$. This shifts the position of equilibrium to the left.
Any increase in $[OH^{-}_{(aq)}]$ is removed in reacting with $H^{+}_{(aq)}$ to form water. The position of equilibrium shifts to the right in order to regenerate the hydrogen ions.

In the body, $H_{2}CO_{3 (aq)}$ can be converted into gaseous $CO_{2}$ which can be exhaled. The rate of breathing controls the amount of $CO_{2}$ in the blood.

Neutralisation

During a titration, an acid is slowly neutralised by adding a base or vice versa. The volume of one solution required to react exactly with the other solution is measured.

Equivalence Point

The point in a titration where the volume of one solution has reacted exactly with the volume of the other solution.

Titration Curves

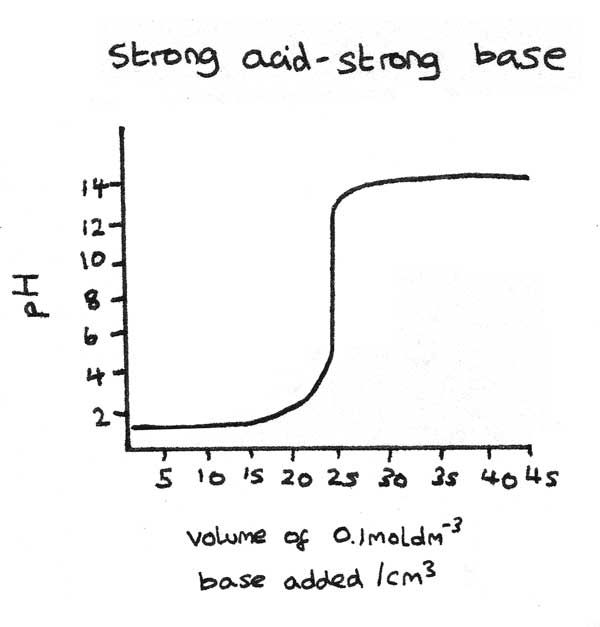
Titration curves show the change in $pH$ when a acid or base is added to another solution. In the example below, an acid is being neutralised through the addition of a base.

Initially the $pH$ only increases very slightly as the acid is in excess.
Close to the equivalence point, the $pH$ increases rapidly. This is shown by the vertical section on the curve. The equivalence point is half way up the vertical section.
As more base is added, the $pH$ increases slowly as the base is now in excess.

titration-curve

Indicators

An acid-base indicator is a weak acid that changes colour across a $pH$ range. This is due to the weak acid and its conjugate base having different colours. The end point is the point in a titration at which there are equal concentrations of the weak acid indicator and conjugate base forms of the indicator.

Titration Curves

In a titration, an indicator is chosen which has an end point as close as possible to the equivalence point of the titration. Different indicators have different $pH$ ranges:

Phenolphthalein: Changes from colourless below $pH~8.2$ to purple above $pH~10$.
Methyl orange: Changes from red below $pH~3.1$ to yellow above $pH~f4.4$.

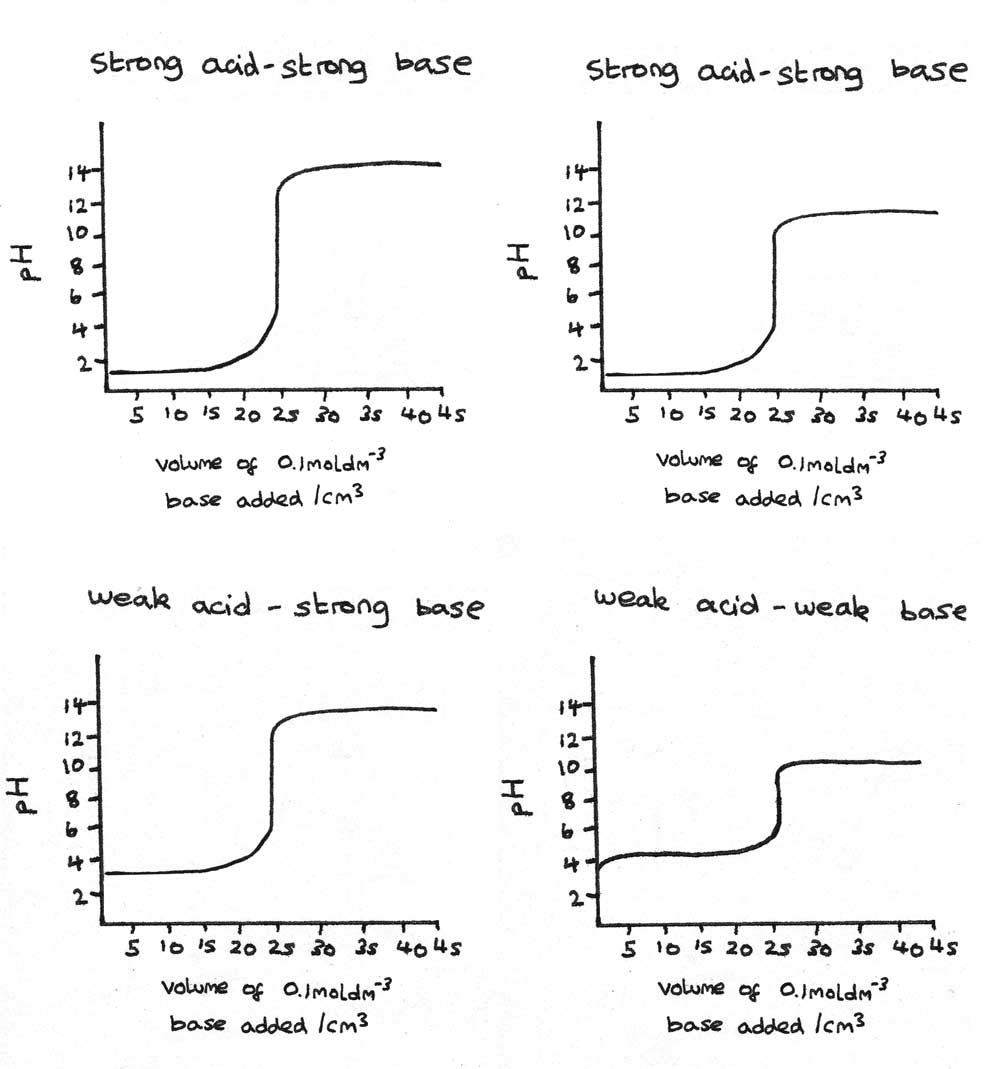
The table below shows the suitability of different indicators in titrations of strong and weak acids with strong and weak bases. When the indicator is suitable, the equivalence point is in the range of the indicator colour change.

	strong acid- strong base	strong acid- weak base	weak acid- strong base
phenolphthalein	suitable	unsuitable	suitable
methyl orange	suitable	unsuitable	suitable

The titration curves below show how the pH changes with added volumes of a base to an acid, for strong and weak acid-base reactions.

titration-curves

Enthalpy Change of Neutralisation

The standard enthalpy change of neutralisation ($\Delta H^{\theta}_{\text{neut}}$) is the enthalpy change when an aqueous acid is neutralised by an aqueous base to form one mole of $H_{2}O_{(l)}$ under standard conditions.

An example of a neutralisation reaction is between hydrochloric acid and sodium hydroxide.

$$ HCl_{(aq)} + NaOH_{(aq)} \rightarrow NaCl_{(aq)} + H_{2}O_{(l)} \hspace{2em} \Delta H^{\theta}_{\text{neut}} = -57.9~kJ mol^{-1} $$

As $Na^{+}_{(aq)}$ and $Cl^{-}_{(aq)}$ act as spectator ions, the ionic equation can be simplified to:
$$ H^{+}_{(aq)} + OH^{-}_{(aq)} \rightarrow H_{2}O_{(l)} $$
The enthalpy change for this reaction is the enthalpy change of neutralisation. The enthalpy change of neutralisation can be determined through an experiment as shown below.

Worked Example

$25.0~cm^{3}$ of dilute nitric acid of concentration $2.00~mol~dm^{-3}$ is added to $25.0~cm^{3}$ of aqueous potassium hydroxide of concentration $2.00~mol~dm^{-3}$. The temperature increases from $22.0°C$ to $35.5°C$.

Calculate the enthalpy change of neutralisation.

Specific heat capacity of solution, $c = 4.18~J~g^{-1}~K^{-1}$.
Density of solution can be assumed to be $1.00~g~cm^{-3}$.

The first stage is to calculate the energy released due to the reaction. This can be done using the formula:
$$ Q = mc\Delta T $$
Where $Q$ is the heat gained by the surroundings ($J$), $m$ is the mass of the solution ($g$), $c$ is the specific heat capacity of solution ($4.18~J~g^{-1}~K^{-1}$) and $\Delta T$ is the change in temperature.
$$ \eqalign{ m &= (25 + 25)(1.00) = 50g \\
\Delta T &= 35.5 - 22.0 = + 13.5°C \\ \\
Q &= (50)(4.18)(13.5) \\
&= + 2821.5~J \\
&= +2.822~kJ } $$
As this is the heat gained by the surroundings, the heat lost by the chemical system is the negative of this value:
$$ Q = -2.822~kJ $$
Next the molar quantities of the acid and base should be calculated in order to scale the energy change for one mole of $H_{2}O_{(l)}$.
$$ \eqalign{\text{moles of } HNO_{3} &= (25.0 \times 10^{-3})(2.00) \\
&= 0.0500~mol \\
\text{moles of } KOH &= (25.0 \times 10^{-3})(2.00) \\
&= 0.0500~mol } $$
The enthalpy change of neutralisation can be calculated by dividing the enthalpy change by the number of moles reacted.

$$ \eqalign{ \Delta H &= \frac{-2.822}{0.0500} \\
&= -56.4~kJ~mol^{-1}} $$

Enthalpy Changes of Neutralisation of Different Acids

Strong Acids

As strong acids completely dissociate, all strong acids share the same ionic equation:
$$ H^{+}_{(aq)} + OH^{-}_{(aq)} \rightarrow H_{2}O_{(l)} $$
This means that all strong acids share a similar value for the enthalpy change of neutralisation ($\Delta H^{\theta}_{\text{neut}}$) around $-57.9 ~kJ~mol^{-1}$.

Weak Acids

Weak acids are only partially dissociated. While the same enthalpy change of neutralisation reaction occurs, energy is usually lost in ionising the acid. An example is breaking the $O-H$ bond in ethanoic acid. This results in a less exothermic enthalpy change of neutralisation.