Born-Haber Cycles
Lattice Enthalpy
In an ionic lattice, strong electrostatic forces hold oppositely charged ions together. Lattice enthalpy is a measure of the strength of these electrostatic forces. Lattice enthalpy $\Delta H^{\theta}_{LE}$ is the enthalpy change when one mole of a solid ionic substance is formed from its gaseous ions under standard conditions.
Standard Conditions
- Pressure of $100~kPa$ (1 atmosphere)
- $298K$ ($25°$)
- $1~mol~dm^{−3}$ for aqueous solutions
Lattice enthalpy is an exothermic reaction as bonds are being formed. A large negative value of lattice enthalpy indicates stronger electrostatic forces between oppositely charged ions in the lattice.
Covalent structures cannot have lattice enthalpies as they are not formed of ions.
Lattice enthalpies cannot be measured directly as it is impossible to form exactly one mole of an ionic lattice from its gaseous ions. By applying Hess’s Law it is possible to calculate the lattice enthalpy through other reaction routes. Some key definitions include:
The standard enthalpy change of formation, $\Delta H^{\theta}_{f}$ is the enthalpy change when one mole of a compound is formed from its constituent elements in their standard states. It is always an exothermic reaction:
$$ K_{(s)} + \tfrac{1}{2}Cl_{2(g)} \rightarrow KCl_{(s)} \hspace{2em} \Delta H^{\theta}_{f} = -437~kJ mol^{-1}$$The standard enthalpy change of atomisation, $\Delta H^{\theta}_{at}$, is the enthalpy change when one mole of gaseous atoms is formed from its element in its standard state. It is always an endothermic reaction:
$$ K_{(s)} \rightarrow K_{(g)} \hspace{2em} \Delta H^{\theta}_{at} = +89~kJ mol^{-1} \\ \tfrac{1}{2}Cl_{2(g)} \rightarrow Cl_{(g)} \hspace{2em} \Delta H^{\theta}_{at} = +121~kJ mol^{-1} $$The first ionisation energy, $\Delta H^{\theta}_{I1}$ is the enthalpy change when one mole of gaseous 1+ ions are formed from one mole of gaseous atoms. It is always an endothermic reaction as the electron being lost most overcome the attraction from the nucleus.
$$ K_{(g)} \rightarrow K^{+}_{(g)} + e^{-} \hspace{2em} \Delta H^{\theta}_{I1} = +419~kJ mol^{-1} $$The second ionisation energy, $\Delta H^{\theta}_{I2}$ is the enthalpy change when one mole of gaseous 2+ ions are formed from one mole of gaseous 1+ ions. It is always an endothermic reaction:
$$ Ca^{+}_{(g)} \rightarrow Ca^{2+}_{(g)} + e^{-} \hspace{2em} \Delta H^{\theta}_{I2} = +1145~kJ mol^{-1} $$The first electron affinity, $\Delta H^{\theta}_{EA1}$ is the enthalpy change when one mole of gaseous 1- ions are formed from one mole of its gaseous atoms. It is always an exothermic reaction:
$$ Cl_{(g)} + e^{-} \rightarrow Cl^{-}_{(g)} \hspace{2em} \Delta H^{\theta}_{EA1} = -349~kJ mol^{-1} $$The second electron affinity, $\Delta H^{\theta}_{EA2}$ is the enthalpy change when one mole of gaseous 2- ions are formed from one mole of its gaseous 1- ions. It is always an endothermic reaction:
$$ O^{-}_{(g)} + e^{-} \rightarrow O^{2-}_{(g)} \hspace{2em} \Delta H^{\theta}_{EA2} = +798~kJ mol^{-1} $$
Born Haber Cycles
A Born-Haber cycle allows for the calculation of an enthalpy change which cannot be measured directly, such as lattice enthalpy. In a Born-Haber cycle, one enthalpy change can be determined from a series of other enthalpy changes. In a cycle, all $\Delta H$ values pointing upwards are endothermic while all $\Delta H$ values pointing downwards are exothermic.
A Born-Haber cycle used to determine the lattice enthalpy of caesium chloride is shown below. The following equations are used to construct the cycle:
- Enthalpy change of formation of $CsCl$:
$$ Cs_{(s)} + \tfrac{1}{2}Cl_{2(g)} \rightarrow CsCl_{(s)} \hspace{2em} \Delta H^{\theta}_{f} = -433~kJ mol^{-1}$$ - Enthalpy change of atomisation of $Cs$:
$$ Cs_{(s)} \rightarrow Cs_{(g)} \hspace{2em} \Delta H^{\theta}_{at} = +73~kJ mol^{-1}$$ - Enthalpy change of atomisation of $Cl$ :
$$ \tfrac{1}{2}Cl_{2(g)} \rightarrow Cl_{(g)} \hspace{2em} \Delta H^{\theta}_{at} = +121~kJ mol^{-1}$$ - First ionisation energy of $Cs$:
$$ Cs_{(g)} \rightarrow Cs^{+}_{(g)} + e^{-} \hspace{2em} \Delta H^{\theta}_{I1} = +376~kJ mol^{-1}$$ - First electron affinity of $Cl$:
$$ Cl_{(g)} + e^{-} \rightarrow Cl^{-}_{(g)} \hspace{2em} \Delta H^{\theta}_{EA1} = -346~kJ mol^{-1}$$
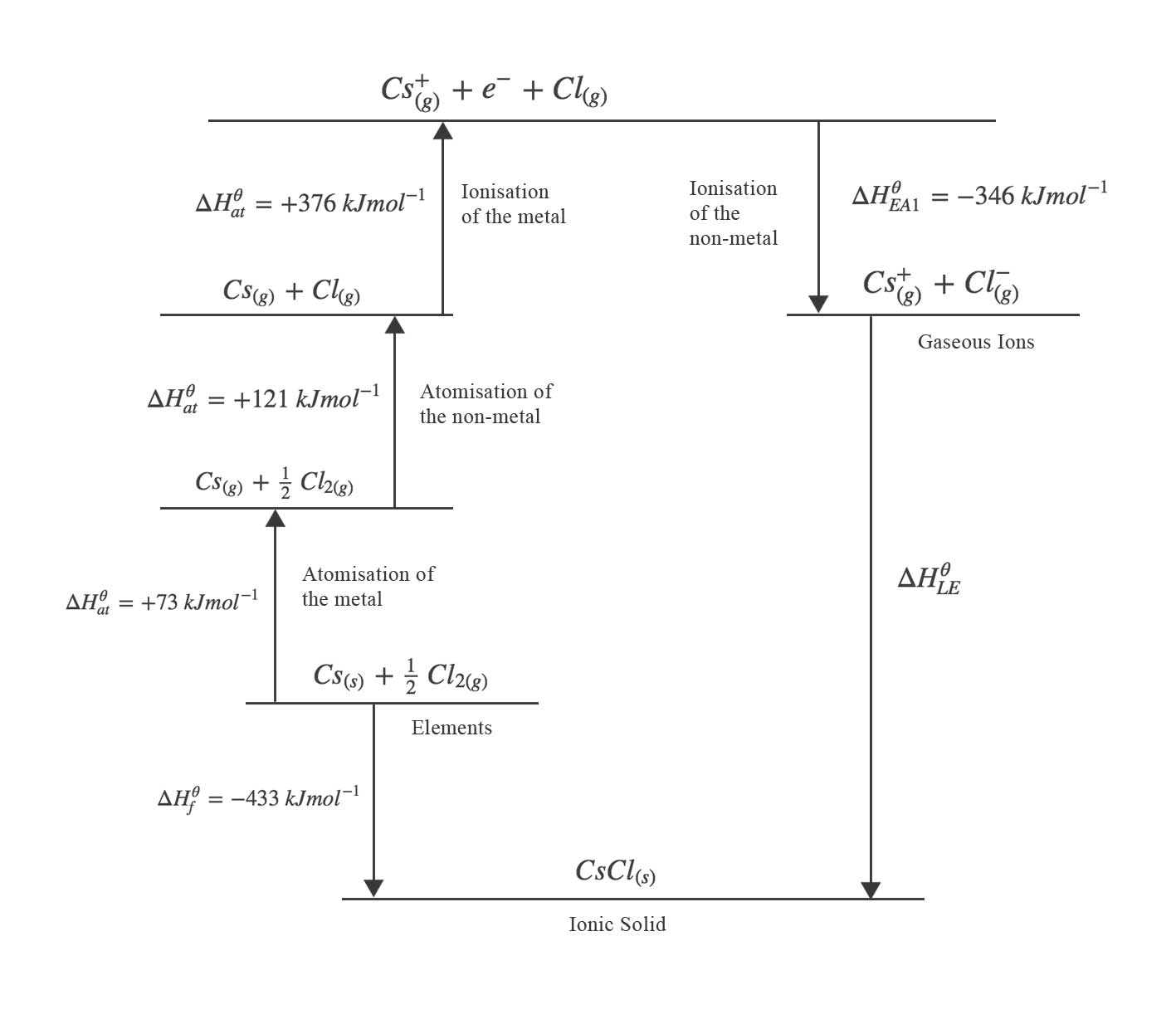
$$ \Delta H^{\theta}_{f} = \text{sum of all other enthalpy changes} \\
-433 = 73 + 121 + 376 - 346 + \Delta H^{\theta}_{LE} \\
\Delta H^{\theta}_{LE} = -657~kJ~mol^{-1}$$
If the lattice enthalpy is known for a Born-Haber cycle, it is possible to calculate the values of other enthalpy changes by substituting known values into the equation and rearranging.
Enthalpy Change of Solution
The standard enthalpy change of solution, $ \Delta H^{\theta}_{s}$ is the enthalpy change when one mole of a solid ionic compound is dissolved to form its aqueous ions under standard conditions. This process can be exothermic or endothermic. For potassium chloride, the reaction is:
$$ KCl_{(s)} + aq \rightarrow K^{+}_{(aq)} + Cl^{-}_{(aq)} $$
When a substance is dissolved:
First the ionic lattice must be broken down by overcoming the attractive electrostatic forces between oppositely charged ions. This process is the opposite of lattice enthalpy so the enthalpy change in breaking down the ionic lattice is $-\Delta H^{\theta}_{LE}$. An example is the breakdown of $KCl_{(s)}$:
$$ KCl_{(s)} \rightarrow K^{+}_{(g)} + Cl^{-}_{(g)}$$Next the generated gaseous ions must be hydrated into aqueous ions. The standard enthalpy change of hydration, $\Delta H^{\theta}_{hyd}$ is the enthalpy change when one mole of aqueous ions are formed from their gaseous ions under standard conditions. It is always an exothermic process. The $\Delta H^{\theta}_{hyd}$ for $K^{+}_{(g)}$ ions is shown below:
$$ K^{+}_{(g)} + aq \rightarrow K^{+}_{(aq)} \hspace{2em} \Delta H^{\theta}_{hyd} = -322~kJ mol^{-1} $$
When constructing Born-Haber cycles using enthalpy change of solution and enthalpy changes of hydration, the following formula can be used to determine the lattice enthalpy:
$$ \Delta H^{\theta}_{LE} + \Delta H^{\theta}_{sol} = \Delta H^{\theta}_{hyd} + \Delta H^{\theta}_{hyd} $$
Worked Example
Using a Born-Haber cycle, calculate the lattice enthalpy of potassium chloride.
$$ \Delta H^{\theta}_{hyd} ~\text{of}~ K^{+}_{(g)} = -322~kJ mol^{-1} \\
\Delta H^{\theta}_{hyd} ~\text{of}~ Cl^{-}_{(g)} = -363~kJ mol^{-1} \\
\Delta H^{\theta}_{s} ~\text{of}~ KCl_{(s)} = +26~kJ mol^{-1} $$
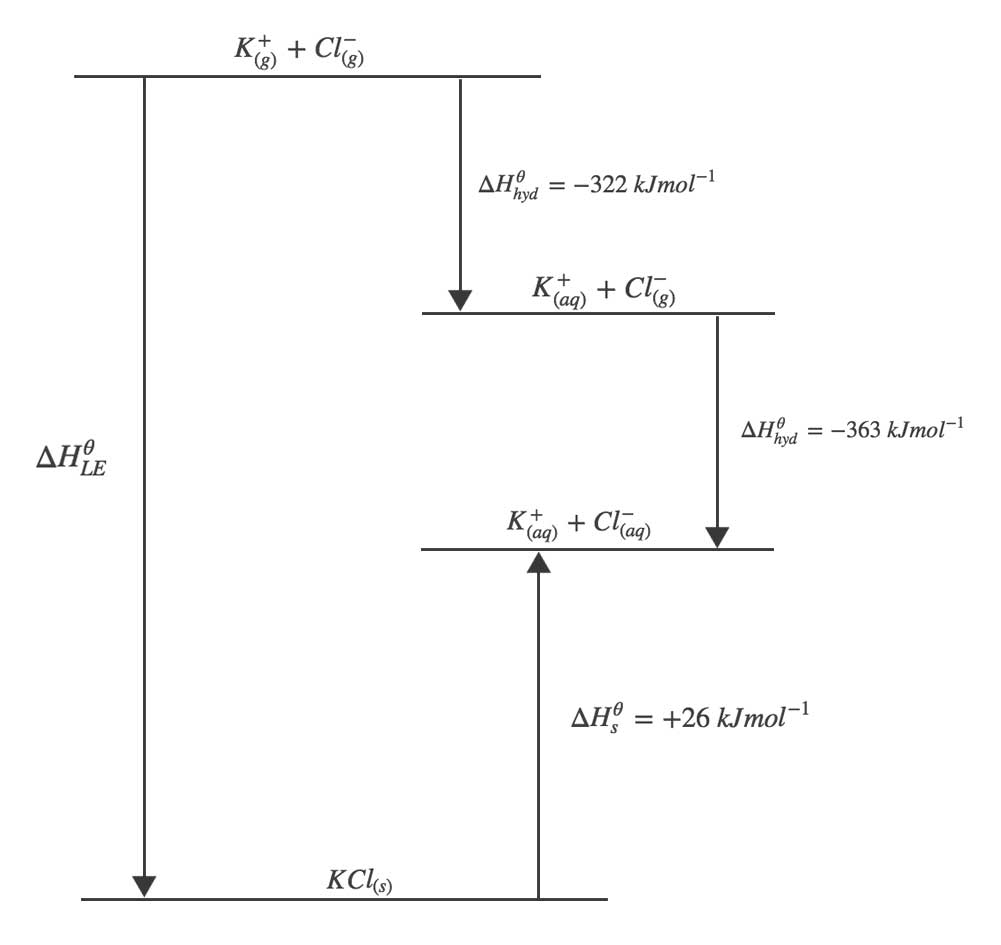
$$ \eqalign{ \Delta H^{\theta}_{LE} + 26 &= -322 - 363 \\
\Delta H^{\theta}_{LE} &= -711~kJmol^{-1} }$$
Factors Affecting Lattice Enthalpy
An ionic solid with large electrostatic forces between oppositely charged ions has a large exothermic lattice enthalpy. The strength of the electrostatic forces depend on the ionic size and charge.
- Ionic size: In an ionic lattice, smaller ions are able to pack more closely together and form stronger ionic bonds. The smaller the ionic radius, the more exothermic the lattice enthalpy.
- Ionic charge: The greater the charge of the ions in an ionic compound, the stronger the electrostatic forces are between them. The greater the ionic charge, the more exothermic the lattice enthalpy.
Factors Affecting $\Delta H^{\theta}_{hyd}$
Like lattice enthalpy, the ionic size and charge also affect the enthalpy change of hydration.
- Ionic size: As the ionic radius decreases, the electrostatic forces increase between the ions and the water molecules become stronger. As the ionic radius decreases, the enthalpy change of hydration becomes more exothermic.
- Ionic charge: As the charge on the ion increases, the electrostatic forces increase between the ions and the water molecules become stronger. As the ionic charge increases, enthalpy change of hydration becomes more exothermic.
Trends in the Periodic Table
- Across a period, the ionic charge increases which reduces the ionic radius. This results in stronger ionic bonds with a more exothermic lattice enthalpy and stronger bonds with the water molecules so a more exothermic $\Delta H^{\theta}_{hyd}$.
- Down a group, the number of nucleons in the ion increases, increasing the ionic radius. With a larger ionic radius, the charge density decreases. This results in weaker ionic bonds with a less exothermic lattice enthalpy and weaker bonds with the water molecules so a less exothermic $\Delta H^{\theta}_{hyd}$.
Entropy
Entropy, $S$ is a measure of disorder in a system. The concept of entropy describes how over time, nature tends to move from a system of order to disorder. As all substances contain particles in constant motion, entropy is always a positive value. Such examples of the tendency to increase disorder include a gas spreading through a room, ice melting in a warm environment or salt dissolving in water. In these examples the energy moves from being localised to more spread out.
Some other examples of entropy changes include:
Reactions where there is a change in the number of gaseous moles. Entropy increases when the number of gaseous molecules increase due to a reaction.
$$ Mg_{(s)} + 2HCl_{(aq)} \rightarrow MgCl_{2(aq)} + H_{2(g)} $$Reactions where there is a change in the number of aqueous moles. Entropy increases when a solid dissolves in a aqueous solution.
$$ CuSO_{4} \cdot 5H_{2}O_{(s)} + aq \rightarrow Cu^{2+}_{(aq)} + SO_{4(aq)}^{2-} + 5H_{2}O_{(l)} $$Reactions where there is a change in state of a compound. Entropy increases during changes in state which give more randomness. This means gases have a much higher entropy than liquids which in turn have a higher entropy than solids. An example is ice melting where the entropy will increase:
$$ H_{2}O_{(s)} \rightarrow H_{2}O_{(l)} $$
Standard Entropy Change of Reaction
The standard entropy, $S^{\ominus}$ of a substance is the entropy content of one mole of a substance under standard conditions. The units of standard entropy are $J~K^{-1}~mol^{-1}$.
The standard entropy change of reaction, $\Delta S$ can be calculated by finding the difference in entropy between the products and the reactants.
$$ \Delta S = \Sigma \Delta S_{\text{(products)}} - \Sigma \Delta S_{\text{(reactants)}} $$
As entropy is a measure of randomness, if a change makes a system more random, the value of $\Delta S$ will be positive.
Worked Example
In this equation, ammonia is formed from nitrogen and hydrogen.
$$ N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)} $$
Looking at the equation, on the left hand side there are four moles of gas while on the right there are only two moles of gas. This would indicate less disorder on the right, so the entropy would be expected to decrease ($\Delta S$ will be $-ve$).
The table below shows the values of standard entropy for the compounds involved in this reaction.
| $N_{2(g)}$ | $H_{2(g)}$ | $NH_{3(g)}$ | |
|---|---|---|---|
| $S^{\ominus} / J~K^{-1}~mol^{-1}$ | $+ 192$ | $+ 131$ | $+ 193$ |
It is important to account for the number of moles of each compound involved in the reaction.
$$ \eqalign{ \Delta S &= \Sigma \Delta S_{\text{(products)}} - \Sigma \Delta S_{\text{(reactants)}} \\
&= (2 \times 193) - (192 + (3 \times 131)) \\
&= -199~J~K^{-1}~mol^{-1} }$$
Spontaneous Processes
A spontaneous process is able to proceed on its own. A process is spontaneous if a chemical system becomes more stable and the overall energy decreases. Both exothermic and endothermic reactions are able to occur spontaneously.
Free Energy
Whether a process is spontaneous or not depends on three factors:
- Temperature, $T$ in kelvin.
- Entropy changes in the system, $\Delta S$.
- Enthalpy changes with the surroundings, $\Delta H$.
The free energy change, $\Delta G$, or change in Gibbs Free Energy is the balance between the temperature, entropy and enthalpy for a process:
$$ \Delta G = \Delta H - T \Delta S $$
Where $\Delta G$ is the change in Gibbs Free Energy ($kJ~mol^{-1}$), $T$ is the temperature in kelvin ($K$) and $\Delta S$ is the change in entropy ($kJ~K^{-1}~mol^{-1}$). Often, the entropy must be converted from $J~K^{-1}~mol^{-1}$ into $kJ~K^{-1}~mol^{-1}$ by dividing the entropy by $1000$.
Feasibility
As a process can only occur spontaneously when the overall energy decreases, $\Delta G$ must be negative for a spontaneous reaction to be feasible:
$$ \Delta G < 0 $$
Worked Example
The equation for the thermal decomposition of ammonium chloride ($NH_{4}Cl$) is shown below:
$$ NH_{4}Cl_{(s)} \rightarrow NH_{3(g)} + HCl_{(g)} \hspace{1em} \Delta H = +176~kJ mol^{-1}$$
Calculate the minimum temperature in $°C$ for thermal decomposition to occur spontaneously. The table below shows the values of standard entropy for the compounds involved in this reaction.
| $NH_{4}Cl_{(s)}$ | $NH_{3(g)}$ | $HCl_{(g)}$ | |
|---|---|---|---|
| $S^{\ominus} / J~K^{-1}~mol^{-1}$ | $+ 95$ | $+ 192$ | $+ 187$ |
First the entropy change must be calculated which can then be substituted in the free energy equation.
$$ \eqalign{ \Delta S &= \Sigma \Delta S_{\text{(products)}} - \Sigma \Delta S_{\text{(reactants)}} \\
&= 192 + 187 - 95 \\
&= + 284~J~K^{-1}~mol^{-1} \\
&= + 0.284~kJ~K^{-1}~mol^{-1}}$$
When the reaction first becomes feasible at the minimum temperature, $\Delta G = 0$,
$$ \eqalign{ \Delta G &= \Delta H - T \Delta S \\
0 &= \Delta H - T \Delta S \\
T &= \frac{\Delta H}{\Delta S} \\
T &= \frac{176}{0.284} \\
T &= 619.7K } $$
To convert the temperature into degrees celsius, $273$ must be subtracted from the temperature in kelvin.
$$ T = 619.7 - 273 = 346.7°C $$