Redox and Half Cells

Redox Equations

In a redox reaction both oxidation and reduction takes place.

Oxidation is the loss of electrons with an increase in oxidation number. A substance that is oxidised is called a reducing agent as it donates electrons to the substance that is being reduced.
Reduction is the gain of electrons with a decrease in oxidation number. A substance that is reduced is called an oxidising agent as it takes electrons from the substance that is being oxidised.

Constructing Redox Equations using Half Equations

Redox equations can be constructed using oxidation and reduction half equations.

Worked Example

Iron reacts with aqueous copper (II) ions to form iron (III) ions and copper metal.

The first step is to construct the two half equations for oxidation and reduction:
$$ \eqalign{ &Fe &\rightarrow Fe^{3+} + 3e^{-} \hspace{1.5em} &\text{Oxidation} \\
&Cu^{2+} + 2e^{-} &\rightarrow Cu \hspace{1.5em} &\text{Reduction}} $$
The half equations must be scaled so the number of electrons is equal in both half equations. In this example, the oxidation half equation must be multiplied by 2 while the reduction half equation must be multiplied by 3.
$$ \eqalign{ &2Fe &\rightarrow 2Fe^{3+} + 6e^{-} \hspace{1.5em} &\text{Oxidation} \\
&3Cu^{2+} + 6e^{-} &\rightarrow 3Cu \hspace{1.5em} &\text{Reduction}} $$
Now the two half equations can be combined into a single redox equation and the electrons can be cancelled:
$$ \eqalign{ 2Fe + 3Cu^{2+} + \cancel{6e^{-}} &\rightarrow 2Fe^{3+} + 3Cu + \cancel{6e^{-}} \\
2Fe + 3Cu^{2+} &\rightarrow 2Fe^{3+} + 3Cu }
$$

Constructing Redox Equations using Oxidation Numbers

Oxidation and reduction can be described in terms of oxidation numbers. Using the oxidation numbers of the individual atoms in a reaction, it is possible to construct a redox equation.

Worked Example

Hydrogen iodide ($HI$) is oxidised to iodine ($I_{2}$) by concentrated sulfuric acid ($H_{2}SO_{4}$) which is reduced to hydrogen sulfide ($H_{2}S$).

First the reactants and the products must be identified from the given information. This allows a draft equation to be formulated. For now, any missing $H$ or $O$ atoms can be ignored.
$$ HI + H_{2}SO_{4} \rightarrow H_{2}S + I_{2} $$
Next the atoms that are undergoing oxidation or reduction must be identified. In this reaction it can be found that $S$ is reduced from $+6$ to $-2$ and $I$ is oxidised from $-1$ to $0$.
$$ \eqalign{
&2HI + H_{2}SO_{4} \rightarrow H_{2}S + I_{2} \\
&\phantom{2HI}~~~~+6 \xrightarrow{~~~-8~~~} -2 \\
&\phantom{}2(-1) \xrightarrow{\hspace{2.6em}+2\hspace{2.6em}} 0 } $$
The reaction must now be balanced so that the total increase in oxidation numbers is equal to the total decrease in oxidation numbers. In this equation, $2HI$ and $I_{2}$ must be multiplied by 4.
$$ \eqalign{
&\phantom{hllo}8HI + H_{2}SO_{4} \rightarrow H_{2}S + 4I_{2} \\
&\phantom{hello124}~~~~+6 \xrightarrow{~~~-8~~~} -2 \\
&4 \times 2(-1) \xrightarrow{\hspace{2.6em}+8\hspace{2.6em}} 4 \times 0 } $$
Finally, all other atoms in the equation must be balanced. For this equation, $4H_{2}O$ should be added to the right hand side of the equation.
$$ 8HI + H_{2}SO_{4} \rightarrow H_{2}S + 4I_{2} + 4H_{2}O$$

After balancing the atoms involved in oxidation and reduction, sometimes the number of $H$ or $O$ may be uneven.

If the reaction has been carried out under acidic conditions $H^{+}$, ions may be added.
If the reaction has been carried out under alkaline conditions, $OH^{-}$ may be added.
If both $H$ and $O$ are missing, $H_{2}O$ should be added.

Cells and Half Cells

An electrochemical cell controls the transfer of electrons to produce electrical energy.

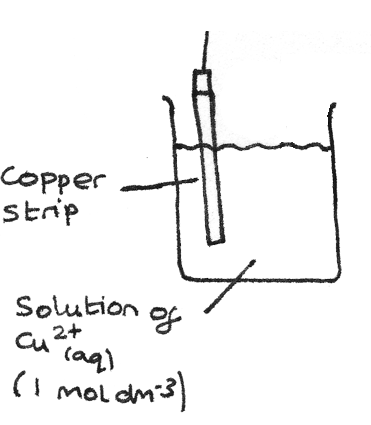
A half cell comprises of an element in two oxidation states. A simple example is a metal placed in an aqueous solution of its ions. If a strip of copper metal ($Cu$) is placed in an aqueous solution containing $Cu^{2+}_{(aq)}$ ions, an equilibrium exists at the surface of the copper strip:

$$ Cu^{2+}_{(aq)} + 2e^{-} \rightleftharpoons Cu_{(s)} $$

The forwards reaction is reduction as electrons are gained while the backwards reaction is oxidation as electrons are being lost. The tendency to gain or lose electrons in the equilibrium of a half cell is known as the electrode potential. A voltmeter placed across two half cells measures the difference in electrode potential.

Metal/Metal Ion Half Cells

The diagram below shows the setup for a half cell of copper strip in a solution of $Cu^{2+}_{(aq)}$ at $1~mol~dm^{-3}$. This half cell is used for an equilibrium with a solid metal and metal ions.
metal_half_cell

Metal ion/Metal ion Half Cells

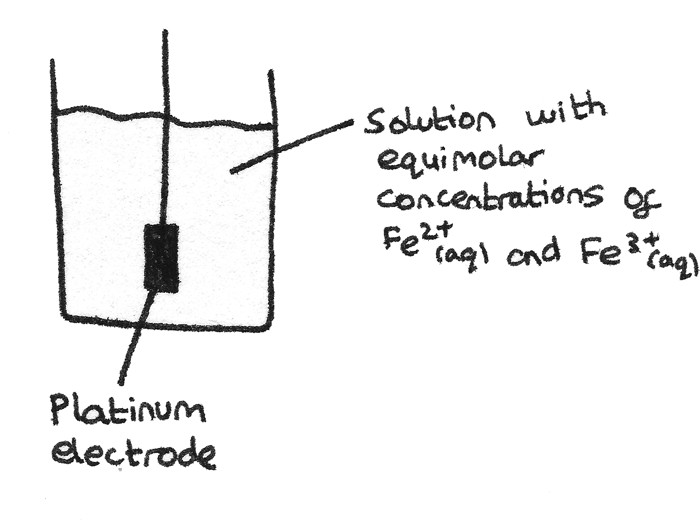
This type of half cell contains a solution of equimolar concentrations of the same element in different oxidation states. An inert platinum electrode allows the transfer of electrons through a connecting wire.

metal_ion_half_cell

Standard Electrode Potential

The standard electrode potential of a half cell, $E^{\ominus}$ is the emf of a half cell compared to a standard hydrogen half cell under standard conditions. Standard conditions are a temperature of $298K$, with $1~mol~dm^{-3}$ concentrations for solutions, at a pressure of $1~atm$. This is used as a reference standard for measuring the emf of a half cell as the standard electrode potential of a hydrogen half cell is defined to be exactly $0V$.

Measuring standard electrode potentials

A standard electrode potential of a cell can be measured by connecting the half cell to a standard hydrogen half cell as shown in the diagram. The voltmeter reading gives the standard electrode potential of the half cell.

standard_electrode_potential
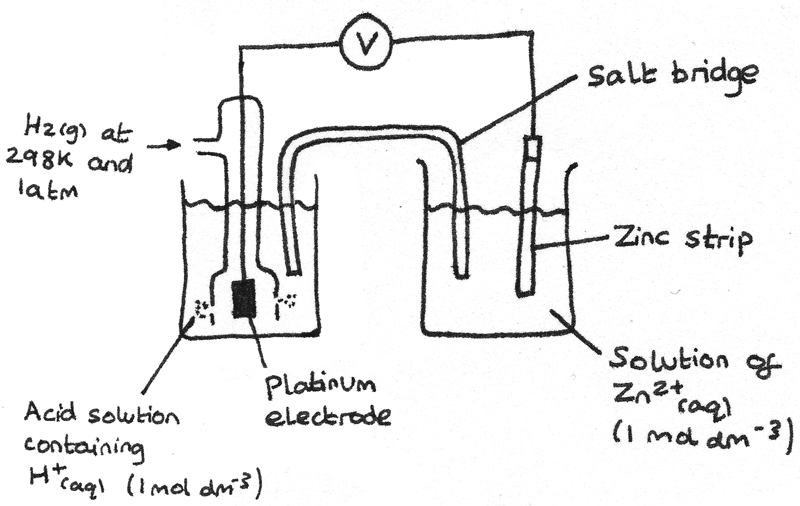
In the example above, the standard electrode potential of the $Zn^{2+}/Zn$ half cell is $-0.76V$. The properties of the standard hydrogen half cell are:

An inert electrode of platinum black on platinum.
A solution of $HCl$ at $1~mol~dm^{-3}$ which acts as a source of $H^{+}$ ions.
Hydrogen gas ($H_{2(g)}$) bubbled into the solution at a pressure of $1~atm$.

The half cell equation for the standard hydrogen half cell is:
$$ 2H^{+}_{(aq)} + 2e^{-} \rightleftharpoons H_{2(g)} $$

Standard Cell Potential

The standard cell potential is the emf between two half cells under standard conditions. It can be calculated by finding the difference between the standard electrode potentials of the half cells.
$$ E^{\ominus}_{\text{cell}} = E^{\ominus}_{\text{(positive terminal)}} - E^{\ominus}_{\text{(negative terminal)}} $$

Electrochemical Cells

Electrochemical cells work on the principle of connecting two half cells together. An example is a cell composed of zinc and copper:
$$ \eqalign{Zn^{2+}_{(aq)} + 2e^{-} &\rightleftharpoons Zn_{(s)} \hspace{1.5em} &E^{\ominus} = -0.76V \\
Cu^{2+}_{(aq)} + 2e^{-} &\rightleftharpoons Cu_{(s)} \hspace{1.5em} &E^{\ominus} = +0.34V }
$$

The diagram below shows the setup for a half cell of copper strip in a solution of $Cu^{2+}_{(aq)}$ at $1~mol~dm^{-3}$ connected to a half cell of zinc strip in a solution of $Zn^{2+}_{(aq)}$ at $1~mol~dm^{-3}$.

The wire allows electrons to be transferred between the two half cells. A current flows through this wire.
A salt bridge allows ions to be transferred between the two solutions. Often aqueous saturated $KNO_{3(aq)}$ or $NH_{4}NO_{3(aq)}$ is used.

metal_metal_half_cells

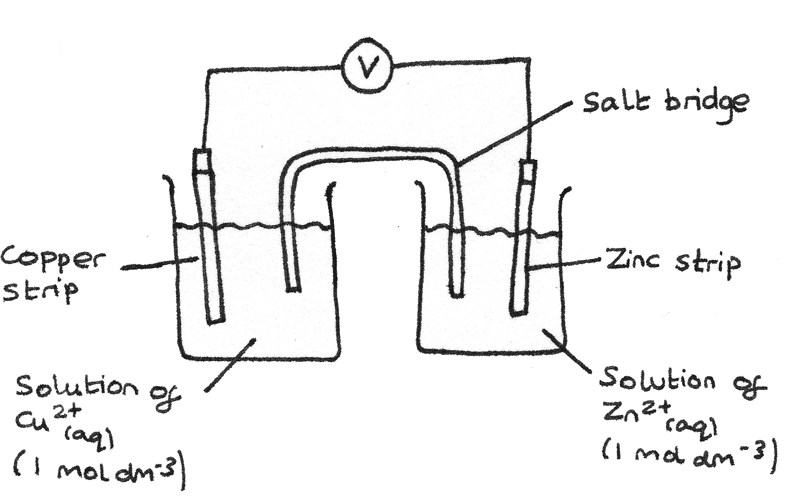
The $Zn^{2+}_{(aq)}$ half cell is the negative terminal and the $Cu^{2+}_{(aq)}$ half cell is the positive terminal. The standard electrode potentials can be used to calculate the emf of the cell:
$$ \eqalign{ E^{\ominus}_{\text{cell}} &= E^{\ominus}_{\text{(positive terminal)}} - E^{\ominus}_{\text{(negative terminal)}} \\
E^{\ominus}_{\text{cell}} &= 0.34 - (-0.76) \\
E^{\ominus}_{\text{cell}} &= 1.10V } $$

Cell Reaction

The cell reaction is the overall reaction taking place within a cell. The half cell with the more negative $E^{\ominus}$ has a greater tendency to lose electrons.

Worked Example

A silver-copper cell is made by connecting together a $Ag_{(s)}/Ag^{+}_{(aq)}$ half cell to a $Cu_{(s)}/Cu^{2+}_{(aq)}$ half cell. The half cell reactions are shown below:
$$ \eqalign{Ag^{+}_{(aq)} + e^{-} &\rightleftharpoons Ag_{(s)} \hspace{1.5em} &E^{\ominus} = +0.80V \\
Cu^{2+}_{(aq)} + 2e^{-} &\rightleftharpoons Cu_{(s)} \hspace{1.5em} &E^{\ominus} = +0.34V }
$$

As the $Cu_{(s)}/Cu^{2+}_{(aq)}$ half cell has a more negative $E^{\ominus}$, it has a greater tendency to lose electrons and act as the negative terminal. The equilibrium shifts to the left:
$$ \xleftarrow{\hspace{5em}} \\ Cu^{2+}_{(aq)} + 2e^{-} \rightleftharpoons Cu_{(s)} $$
The $Ag_{(s)}/Ag^{+}_{(aq)}$ half cell has a more positive $E^{\ominus}$ so it acts as the positive terminal. The equilibrium shifts to the right:
$$ \xrightarrow{\hspace{5em}} \\ Ag^{+}_{(aq)} + e^{-} \rightleftharpoons Ag_{(s)} $$

The equations taking place at each electrode are shown below:
$$ \eqalign{ Cu_{(s)}\phantom{ + e^{-}} &\rightarrow Cu^{2+}_{(aq)} + 2e^{-} \\
Ag^{+}_{(aq)} + e^{-} &\rightarrow Ag_{(s)}} $$

In order to balance the electrons, the $Ag_{(s)}/Ag^{+}_{(aq)}$ half cell equation must be multiplied by 2:
$$ \eqalign{ Cu_{(s)}\phantom{ + e^{-}} &\rightarrow Cu^{2+}_{(aq)} + 2e^{-} \\
2Ag^{+}_{(aq)} + 2e^{-} &\rightarrow 2Ag_{(s)}} $$

The two half cell equations can now be combined into a single cell equation:
$$ \eqalign{ Cu_{(s)} + 2Ag^{+}_{(aq)} + \cancel{2e^{-}} &\rightarrow Cu^{2+}_{(aq)} + 2Ag_{(s)} + \cancel{2e^{-}} \\
Cu_{(s)} + 2Ag^{+}_{(aq)} &\rightarrow Cu^{2+}_{(aq)} + 2Ag_{(s)} }
$$

Feasibility of Reactions

The electrochemical series consists of several redox equilibria ordered by standard electrode potentials. Conventionally, the electrons are shown on the left hand side of the redox equilibrium. Some redox equilibria are shown below:

$$ \eqalign{
Fe^{2+}_{(aq)} + 2e^{-} &\rightleftharpoons Fe_{(s)} \hspace{1.5em} &E^{\ominus} = -0.44V \\
2H^{+}_{(aq)} + 2e^{-} &\rightleftharpoons H_{2(g)} \hspace{1.5em} &E^{\ominus} = 0V \\
Cu^{2+}_{(aq)} + 2e^{-} &\rightleftharpoons Cu_{(s)} \hspace{1.5em} &E^{\ominus} = +0.34V \\
Br_{2(g)} + 2e^{-} &\rightleftharpoons 2Br^{-}_{(aq)} \hspace{1.5em} &E^{\ominus} = +1.07V \\
Cl_{2(g)} + 2e^{-} &\rightleftharpoons 2Cl^{-}_{(aq)} \hspace{1.5em} &E^{\ominus} = +1.36V
} $$

The higher up the list, the more negative the standard electrode potential and the greater the tendency to release electrons and shift the equilibrium to the left.

This means that any species on the right of the above equilibria are able to react with every species below and on the left. This is because the position of equilibrium of the more negative electrode is to the left while the position of equilibrium of the more positive electrode is to the right.
$Fe_{(s)}$ would react with $H^{+}_{(aq)}$, $Cu^{2+}_{(aq)}$, $Br_{2(g)}$ and $Cl_{2(g)}$.
$Cu_{(s)}$ would only react with $Br_{2(g)}$ and $Cl_{2(g)}$.

Limitations of Predictions using Standard Electrode Potentials

As temperature and concentration affect the position of equilibrium, changes during a reaction can result in non standard conditions and different electrode potentials.
A reaction may have a slow rate of reaction due to a very high activation energy making it unfeasible.

Generally the greater the difference in $E^{\ominus}$ values between the electrodes, the more likely the reaction is to take place.

Cells and batteries

Electrochemical cells are commonly used in batteries and cells:

Non rechargeable cells such as disposable batteries only have a fixed lifespan after which the voltage falls.
Rechargeable cells such as nickel and cadmium batteries and lithium polymer batteries which are used in laptops. The cell reaction can be reversed which regenerates the chemicals in the cell.
Fuel cells which use an external supply of a fuel and an oxidant.

Fuel Cells

A fuel cell uses a reaction of a fuel with oxygen to produce a voltage. Fuel cells are able to run continuously as long as there is an oxidant and fuel supply into the cell. A fuel cell consists of an electrolyte between two electrodes.

fuel_cell

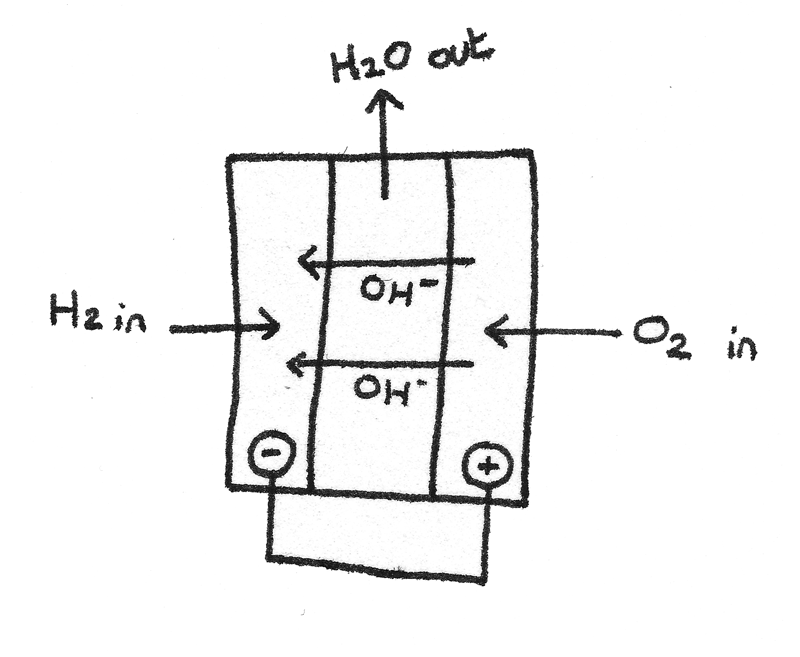
An alkaline hydrogen-oxygen fuel cell uses hydrogen and oxygen to produce a voltage. A aqueous alkaline solution such as $KOH_{(aq)}$ is used as the electrolyte. The half cell reactions are shown below:
$$ \eqalign{2H_{2}O_{(l)} + 2e^{-} &\rightleftharpoons H_{2(g)} + 2OH^{-}_{(aq)} \hspace{1.5em} &E^{\ominus} = -0.83V \\
\frac{1}{2}O_{2(g)} + H_{2}O_{(l)} + 2e^{-} &\rightleftharpoons 2OH^{-}_{(aq)} \hspace{1.5em} &E^{\ominus} = +0.40V }
$$

The emf of the cell can be calculated by finding the difference between the two half cells. By combining the two equations together, the overall reaction can be given as:
$$ H_{2(g)} + \frac{1}{2}O_{2(g)} \rightarrow H_{2}O_{(l)} $$

Proton Exchange Membrane Cell

A polymer membrane electrolyte can be used where $H^{+}$ ions diffuse through an ion-permeable membrane. The half cell equations are:
$$ \eqalign{2H^{+}_{(aq)} + 2e^{-} &\rightleftharpoons H_{2(g)} \hspace{1.5em} &E^{\ominus} = 0.00V \\
\frac{1}{2}O_{2(g)} + 2H^{+}_{(aq)} + 2e^{-} &\rightleftharpoons H_{2}O_{(l)} \hspace{1.5em} &E^{\ominus} = +1.23V }
$$
The overall cell equation is the same as the the alkaline fuel cell:
$$ H_{2(g)} + \frac{1}{2}O_{2(g)} \rightarrow H_{2}O_{(l)} $$

Fuel Cell Vehicles

Fuel cells are being developed as an alternative to finite oil based fuels in cars. Fuel cell vehicles (FCVs) use hydrogen rich fuels such as methanol or methane. An onboard reformer extracts the hydrogen gas which can be fed into the fuel cell:
$$ CH_{3}OH + H_{2}O \rightarrow 3H_{2} + CO_{2} $$
This has the benefits of:

A liquid fuel is easier and safer to transport in vehicles than compressed hydrogen gas.
Methanol can be generated from biomass.

Direct methanol fuel cells are also being developed where the methanol acts as the fuel. A polymer membrane electrolyte is used.
$$
\eqalign{
6e^{-} + 6H^{+} + CO_{2(g)} &\rightleftharpoons CH_{3}OH_{(l)} + H_{2}O_{(l)} \\
6e^{-} + \frac{3}{2}O_{2(g)} + 6H^{+}_{(aq)} &\rightleftharpoons 3H_{2}O_{(l)}
}
$$
This gives an overall reaction of:
$$ \frac{3}{2}O_{2(g)} + CH_{3}OH_{(l)} \rightleftharpoons CO_{2(g)} + 2H_{2}O_{(l)} $$

Advantages of Fuel Cell Vehicles

Hydrogen rich fuels only produce small amounts of $CO_{2}$ and other air pollutants compared to conventional hydrocarbon fuels. If hydrogen gas is used, the only byproduct is water.
Hydrogen fuel cells are more efficient in converting the fuel into useful energy. Petrol engines waste a large amount of the chemical energy as heat.

Storage of Hydrogen

As hydrogen is a gas with a very low boiling point, storage is a problem compared to liquid fuels such as petrol and diesel. Some methods of storage include:

Storage as a liquid under high pressure at a very low temperature.
Hydrogen can be adsorbed onto the surface of a material.
Hydrogen can be absorbed as hydrides into a solid lattice.

More research is being done to overcome concerns about the feasibility of storing a pressurised liquid and the fact that current absorbers and adsorbers of hydrogen only have a limited lifespan.

Limitations of Hydrogen Fuel Cells

Hydrogen is a colourless, odourless and flammable gas with small molecules which have the potential to leak easily.
A large scale infrastructure must be set up to deliver and store the hydrogen. There are logistical problems associated with the maintenance and handing of hydrogen.
Fuel cells only have a limited lifespan, requiring regular maintenance which can be expensive to the consumer.
Fuel cells use toxic chemicals in their production.
Energy must be used in order to extract hydrogen either through the hydrolysis of water or by reacting methane which is a finite fuel with steam.