Transition Metals
Transition Metals
The d-block elements are found in between group 2 and group 3 in the periodic table. The highest electron energy sub-shell in these elements is a d sub-shell. A transition element is a d-block element that forms at least one ion with an incomplete d sub-shell.
Scandium and zinc are not transition metals as they are unable to generate ions with an incomplete d sub-shell.
Electron Configurations
Electron configurations show the arrangement of electrons in an atom of an element. The electron configuration for titanium is shown below:
$$ 1s^{2}~2s^{2}~2p^{6}~3s^{2}~3p^{6}~4s^{2}~3d^{2} $$
Normally, the $4s$ is completely filled before the $3d$ sub-shell. However for chromium and copper, the $4s$ sub-shell only contains one electron. The half filled d sub-shell in chromium and the full d sub-shell in copper results in a more stable configuration.
$$ Cr: 1s^{2}~2s^{2}~2p^{6}~3s^{2}~3p^{6}~4s^{1}~3d^{5} \\
Cu: 1s^{2}~2s^{2}~2p^{6}~3s^{2}~3p^{6}~4s^{1}~3d^{10} $$
This arrangement has a greater stability as there is less repulsion between outer shell electrons. The $Cr$ has a half filled d sub-shell while $Cu$ has a totally filled d sub-shell.
Ions
Transition metals form ions by first losing electrons from the $4s$ sub-shell before the $3d$ sub-shell. This is because after the electrons occupy the orbitals, the $4s$ energy level rises to a higher energy level.
The electron configurations for $Fe^{3+}$ and $Fe$ are shown below:
$$ \eqalign{ Fe: &1s^{2}~2s^{2}~2p^{6}~3s^{2}~3p^{6}~4s^{2}~3d^{6} \\
Fe^{3+}: &1s^{2}~2s^{2}~2p^{6}~3s^{2}~3p^{6}~3d^{5}} $$
Transition Metal Properties
- Transition metals all display typical metallic properties. These include a high melting point, high boiling point, shiny appearance and good electrical conductivity.
- The transition metals are able to form ions with variable oxidation states. All the transition metals are able to form $2+$ ions typically by removing the two electrons from the $4s$ sub-shell. However most can also lose more electrons.
- Transition metals are able to form coloured compounds. The colour is linked to the partially filled d sub-shell. Colour changes in reactions involving transition metals can help to identify compounds.
- Transition metals can act as effective catalysts.
Catalysis
A catalyst is a substance that increases the rate of a reaction by lowering the activation energy. Transition metals are very effective catalysts:
- They can provide a surface for a reaction to take place on, as they are able to bond to a wide range of ions and molecules.
- Due to their ability to have variable oxidation states, they can bind to reactants and form intermediates as part of a chemical pathway with a lower activation energy.
Below are some examples of reactions where a transition metal acts as a catalyst:
Haber Process
The Haber process is used to make ammonia ($NH_{3}$), from hydrogen and nitrogen. The produced ammonia is often used for fertilisers.
$$ N_{2(g)} + 3H_{2(g)} \rightleftharpoons 2NH_{3(g)} $$
Iron metal is used as the catalyst to increase the rate of reaction and reduce the required temperature.
Contact Process
The contact process is used to convert sulphur dioxide ($SO_{2}$) into sulphur trioxide ($SO_{3}$) which is used in producing sulphuric acid ($H_{2}SO_{4}$).
$$ 2SO_{2(g)} + O_{2(g)} \rightleftharpoons 2SO_{3(g)} $$
Vanadium(V) oxide ($V_{2}O_{5}$) is used as the catalyst where vanadium has an oxidation state of $5+$.
Transition metals are used as catalysts in other processes such as nickel metal in the hydrogenation of alkenes and manganese(IV) oxide in the decomposition of hydrogen peroxide.
Precipitation Reactions
Upon reacting transition metal ions with hydroxide ions, such as from $NaOH_{(aq)}$, a solid coloured precipitate is formed. Some precipitation reactions are shown below:
A blue solution containing $Cu^{2+}_{(aq)}$ reacts to form a blue precipitate, copper(II) hydroxide.
$$ Cu^{2+}_{(aq)} + 2OH^{-}_{(aq)} \rightarrow Cu(OH)_{2(s)} $$A pink solution containing $Co^{2+}_{(aq)}$ forms a blue precipitate, cobalt(II) hydroxide.
$$ Co^{2+}_{(aq)} + 2OH^{-}_{(aq)} \rightarrow Co(OH)_{2(s)} $$A pale green solution containing $Fe^{2+}_{(aq)}$ forms a green precipitate, iron(II) hydroxide. If left in air, $Fe^{2+}_{(aq)}$ ions are readily oxidised to $Fe^{3+}_{(aq)}$, forming a brown colour at the surface of the precipitate.
$$ Fe^{2+}_{(aq)} + 2OH^{-}_{(aq)} \rightarrow Fe(OH)_{2(s)} $$A pale yellow solution containing $Fe^{3+}_{(aq)}$ forms a brown precipitate, iron(III) hydroxide.
$$ Fe^{3+}_{(aq)} + 3OH^{-}_{(aq)} \rightarrow Fe(OH)_{3(s)} $$
Complex Ions
Transition metals are able to form complex ions. Some definitions regarding transition metals are listed below:
- Complex ion: A transition metal ion consisting of a central metal ion surrounded by ligands.
- Ligand: A molecule or ion which donates a pair of electrons to a transition metal ion, forming a coordinate bond.
- Coordination number: The total number of coordinate bonds formed between a central metal ion and any other ligands.
An example of a complex ion is $[Cu(H_{2}O)_{6}]^{2+}$. The central metal ion is $Cu^{2+}$, surrounded by six $H_{2}O$ ligands. This complex ion has a coordinate number of $6$ as there are $6$ coordinate bonds formed between the ligands and the central metal ion.
Types of Ligands
Ligands can be neutral or negatively charged. All ligands have at least one pair of electrons, able to form a coordinate bond with the transition metal ion.
- Monodentate ligands donate one pair of electrons.
- Bidentate ligands are able to donate two pairs of electrons and form two coordinate bonds.
- Multidentate ligands are able to donate many pairs of electrons and form multiple coordinate bonds. $EDTA^{4-}$ is a hexadentate ligand able to form six coordinate bonds by donating six pairs of electrons.
Some common types of ligands are listed below:
| Name | Formula | Type |
|---|---|---|
| Water | $H_{2}O$ | Monodentate |
| Ammonia | $NH_{3}$ | Monodentate |
| Chloride Ion | $Cl^{-}$ | Monodentate |
| Hydroxide Ion | $OH^{-}$ | Monodentate |
| Cyanide Ion | $CN^{-}$ | Monodentate |
| Ethane-1,2-diamine (en) | $H_{2}NCH_{2}CH_{2}NH_{2}$ | Bidentate |
| $EDTA^{4-}$ | - | Hexadentate |
Shapes of Complex Ions
Some shapes of common complex ions are shown below.
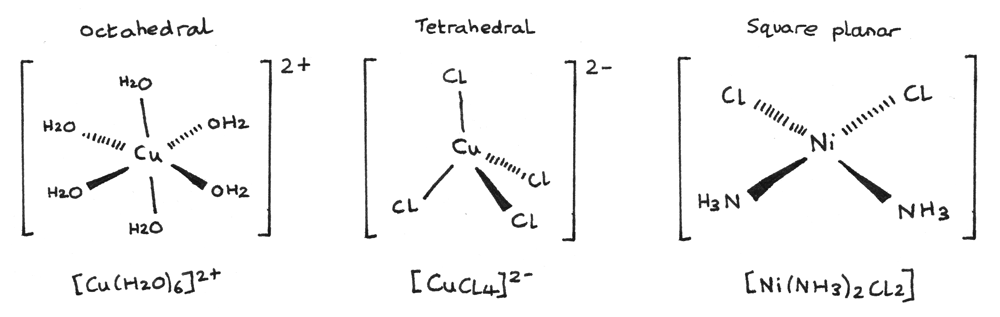
- $[Cu(H_{2}O)_{6}]^{2+}$ is an octahedral complex with a coordination number of $6$. The bond angles are $90°$. The octahedral shape is the most common shape of complex ion. The central $Cu^{2+}$ has a $2+$ oxidation state while the $H_{2}O$ ligands are neutral.
- $[CuCl_{4}]^{2-}$ is an tetrahedral complex with a coordination number of $4$. The bond angles are $109.5°$. The central $Cu^{2+}$ has a $2+$ oxidation state, while the surrounding $Cl^{-}$ ligands have a $1-$ oxidation state.
- $[Ni(NH_{3})_{2}Cl_{2}]$ is a square planar complex with a coordination number of $4$. The bond angles are $90°$. The central $Ni^{2+}$ has a $2+$ oxidation state, while the surrounding $Cl^{-}$ ligands have a $1-$ oxidation state and the $NH_{3}$ ligands are neutral.
Isomerism
Stereoisomers are species with the same structural formula but different arrangement of atoms in space. Transition metals can display both cis-trans isomerism and optical isomerism.
Cis-Trans Isomerism
Cis-trans isomerism in complex ions depends on the arrangement of the ligands around a central metal ion.
Octahedral Complexes
Octahedral complexes that contain six monodentate ligands such that there are four of one type of ligand and two of another ligand, are able to form cis-trans isomers. An example is shown below:
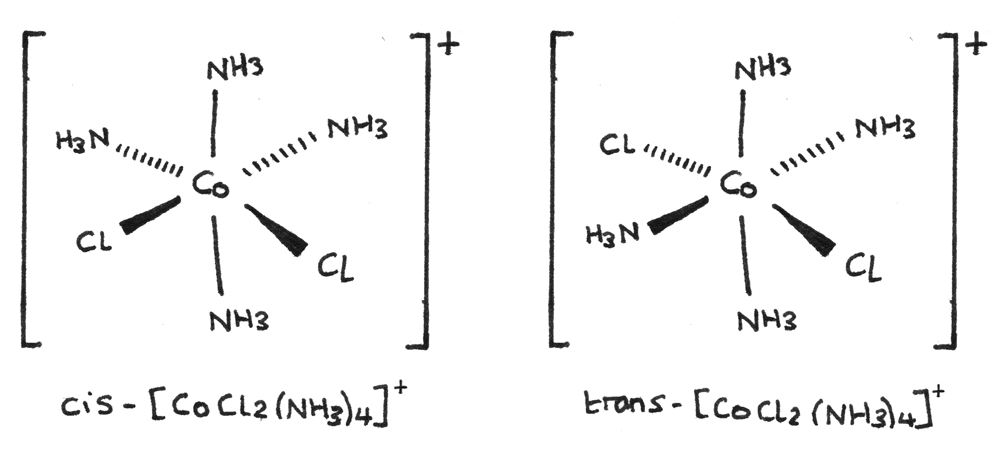
- The cis form of the isomer has a $90°$ bond angle between the two $Cl^{-}$ ligands.
- The trans form of the isomer has a $180°$ bond angle between the two $Cl^{-}$ ligands.
Square planar Complexes
Square planar complexes that contain two of one type of ligand and two of another type of ligand can form cis-trans isomers. They often contain a $Ni^{2+}$ or $Pt^{2+}$ central metal ion. An example is shown below:
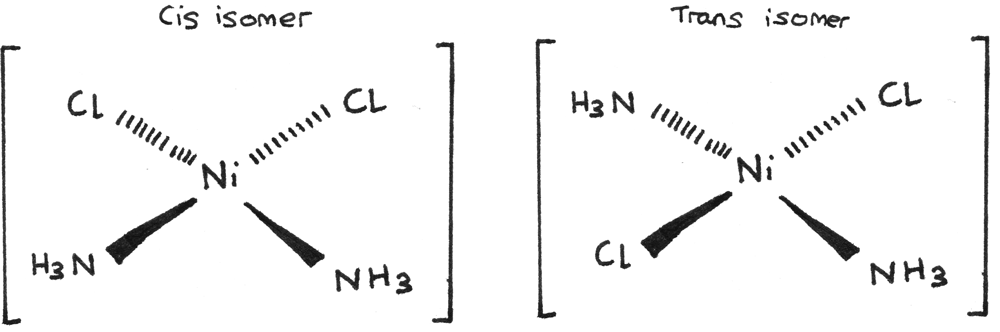
A stereoisomer of another square planar complex, platin $[Pt(Cl)_{2}(NH_{3})_{2}]$ is used as an anti cancer drug. Cis-platin binds to the DNA in fast growing cancer cells, preventing replication and cell division.
Bidentate ligands
Octahedral complexes containing bidentate ligands can show cis-trans isomerism. An example is shown below:
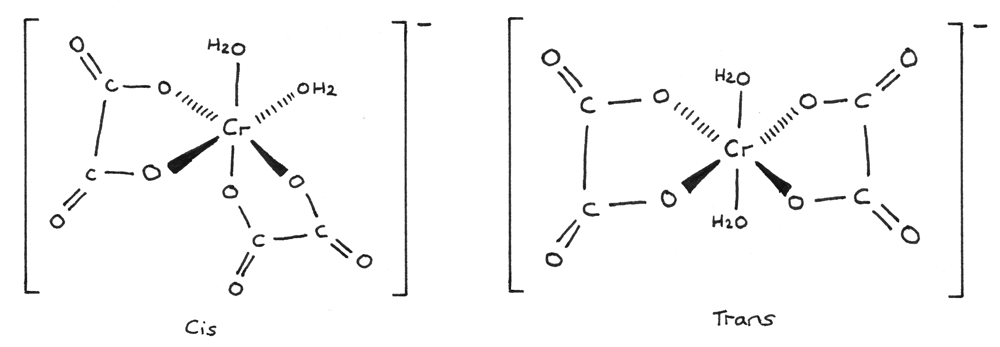
- The cis-form of the isomer has a $90°$ bond angle between the two monodentate ligands.
- The trans-form of the isomer has a $180°$ bond angle between the two monodentate ligands.
Optical Isomerism
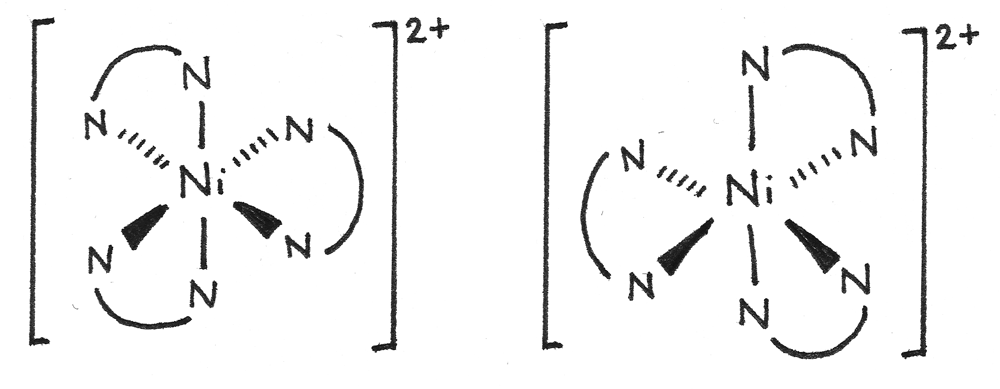
Optical isomers are two non-superimposable mirror images of each other. The requirements for optical isomerism in octahedral complex ions are:
- A complex ion with three bidentate ligands, for example $[Ni(en)_{3}]^{2+}$.
- A complex ion with two bidentate ligands, and two other monodentate ligands. An example is $[Co(en)_{2}Cl_{2}]$.
- A complex ion with a hexadentate ligand, for example $[Cu(EDTA)]^{2-}$.
An example of optical isomerism is shown below for $[Ni(en)_{3}]^{2+}$:
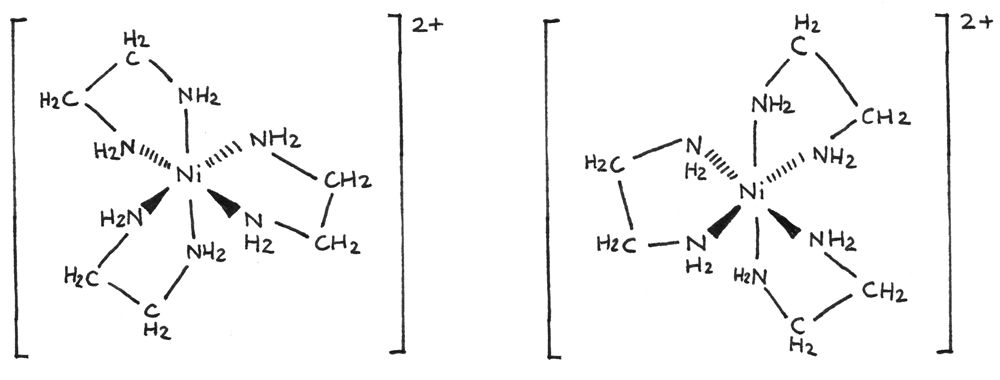
A simplified diagram can also be used to show the optical isomerism:
Ligand Substitution
Ligand substitution is a reversible reaction where a ligand in a complex ion is replaced by another ligand. These reactions can be observed through colour changes.
Aqueous Copper(II) ions and Ammonia
In this reaction, aqueous $NH_{3}$ molecules substitute the $H_{2}O$ ligands in the $[Cu(H_{2}O)_{6}]^{2+}$ complex ion.
$$ \eqalign{&[Cu(H_{2}O)_{6}]^{2+}_{(aq)} + 4NH_{3(aq)} \rightleftharpoons &[Cu(NH_{3})_{4}(H_{2}O)_{2}]^{2+}_{(aq)} + 4H_{2}O_{(l)} \\
&\text{Pale blue solution} &\text{Deep blue solution}} $$
When an excess of ammonia solution is added, the pale blue solution changes colour forming a deep blue solution.
Aqueous Copper(II) ions and Hydrochloric Acid
In this reaction, $Cl^{-}$ ions replace the $H_{2}O$ ligands in the $[Cu(H_{2}O)_{6}]^{2+}$ complex ion. As chlorine atoms are much larger than water molecules, the octahedral complex ion takes up a tetrahedral shape after the substitution.
$$ \eqalign{&[Cu(H_{2}O)_{6}]^{2+}_{(aq)} + 4Cl^{-}_{(aq)} \rightleftharpoons &[CuCl_{4}]^{2-}_{(aq)} + 6H_{2}O_{(l)} \\
&\text{Pale blue solution} &\text{Yellow solution}} $$
When the concentrated hydrochloric acid is added, the pale blue solution first turns green before turning yellow. The green intermediate is due to the mixing of the blue and yellow solutions during the equilibrium.
Cobalt(II) ions and Hydrochloric Acid
In this reaction $Cl^{-}$ ions replace the $H_{2}O$ ligands in the $[Co(H_{2}O)_{6}]^{2+}$ complex ion.
$$ \eqalign{&[Co(H_{2}O)_{6}]^{2+}_{(aq)} + 4Cl^{-}_{(aq)} \rightleftharpoons &[CoCl_{4}]^{2-}_{(aq)} + 6H_{2}O_{(l)} \\
&\text{Pale pink solution} &\text{Blue solution}} $$
When the concentrated hydrochloric acid is added, the pale pink solution changes colour forming a blue solution.
Haemoglobin
Red blood cells in the human body contain haemoglobin which transports oxygen around the body through ligand substitution. Haemoglobin contains a $Fe^{2+}$ complex ion which can form a coordinate bond with oxygen. The oxygen can then be transported and released in other parts of the body.
Carbon monoxide is a toxic, odourless and colourless gas which binds more strongly to haemoglobin than oxygen. When this irreversible ligand substitution occurs, less haemoglobin is able to transport oxygen around the blood which can cause asphyxiation, due to the lack of oxygen.
Stability Constant
When a ligand is added to an aqueous solution of a complex ion formed between water and a transition metal ion, an equilibrium is set up. The equilibrium constant for this equilibrium is known as the stability constant, $K_{\text{stab}}$.
Stability Constant
The stability constant, $K_{\text{stab}}$ is the equilibrium constant for an equilibrium existing between a transition metal ion surrounded by water ligands and the complex ion formed when the same ion has undergone ligand substitution.
When chloride ions are added to an aqueous solution of $Co^{2+}$ ions, the following equilibrium is set up:
$$ [Co(H_{2}O)_{6}]^{2+}_{(aq)} + 4Cl^{-}_{(aq)} \rightleftharpoons [CoCl_{4}]^{2-}_{(aq)} + 6H_{2}O_{(l)} $$
The stability constant, $K_{\text{stab}}$ for $[CoCl_{4}]^{2-}_{(aq)}$ can be shown as:
$$ K_{\text{stab}} = \frac{[[CoCl_{4}]^{2-}_{(aq)}]}{[[Co(H_{2}O)_{6}]^{2+}_{(aq)}][Cl^{-}_{(aq)}]^{4}} $$
The water is left out of the expression for $K_{\text{stab}}$ as it is in a large excess with its value nearly constant.
Interpreting $K_{\text{stab}}$
A large value of $K_{\text{stab}}$ indicates that the position of equilibrium lies to the right. This means that the complex ion is more readily formed. The higher the value of stability constant, the more stable the complex ion.
Worked Example
Chloride ions ($Cl^{-}_{(aq)}$) are added to an aqueous solution of $[Cu(H_{2}O)_{6}]^{2+}_{(aq)}$. The following equilibrium is set up:
$$ [Cu(H_{2}O)_{6}]^{2+}_{(aq)} + 4Cl^{-}_{(aq)} \rightleftharpoons [CuCl_{4}]^{2-}_{(aq)} + 6H_{2}O_{(l)} $$
At $25°C$, the equilibrium mixture contains $1.17 \times 10^{-5}~mol~dm^{-3}$ $[Cu(H_{2}O)_{6}]^{2+}_{(aq)}$, $0.800~mol~dm^{-3}$ $Cl^{-}_{(aq)}$ and $2.00~mol~dm^{-3}$ $[CuCl_{4}]^{2-}_{(aq)}$. Calculate the $K_{\text{stab}}$.
The first step is to write an expression for $K_{\text{stab}}$:
$$ K_{\text{stab}} = \frac{[[CuCl_{4}]^{2-}_{(aq)}]}{[[Cu(H_{2}O)_{6}]^{2+}_{(aq)}][Cl^{-}_{(aq)}]^{4}} $$Next the concentrations can be inserted into the equation:
$$ \eqalign{ K_{\text{stab}} &= \frac{2.00}{(1.17 \times 10^{-5}) \times (0.800)^{4}} \\
K_{\text{stab}} &= 4.17 \times 10^{5}} $$The units for $K_{\text{stab}}$ should also be calculated. The units for the concentrations are $mol~dm^{-3}$.
$$ \frac{mol~dm^{-3}}{(mol~dm^{-3})(mol~dm^{-3})^{4}} = dm^{12}~mol^{-4} $$
The final answer is therefore $K_{\text{stab}} = 4.17 \times 10^{5}~dm^{12}~mol^{-4}$.