Equilibrium
Le Chatelier's Principle
Le Chatelier's principle states that when any changes are made to the conditions of a system in dynamic equilibrium, the position of equilibrium shifts in order to oppose the change.
Dynamic Equilibrium
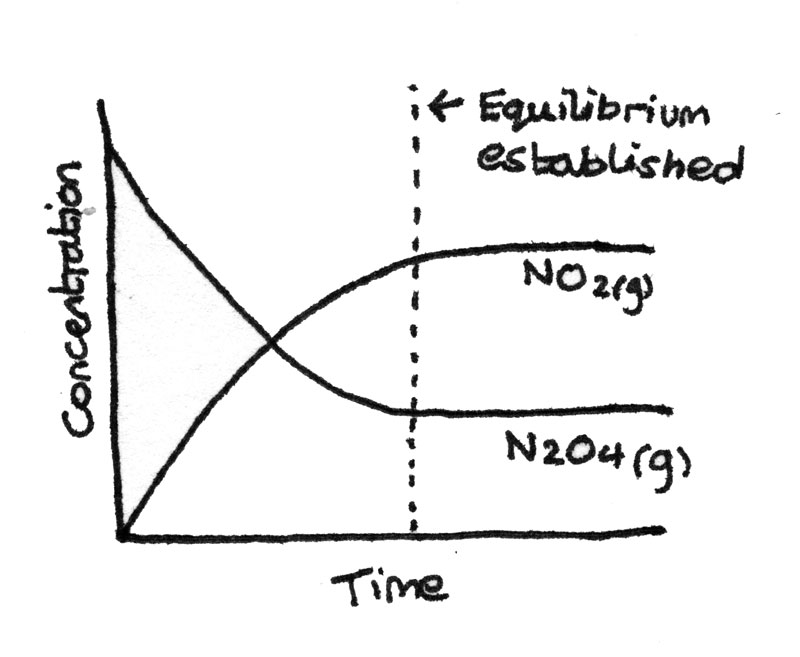
Dynamic equilibrium is established in a closed system when the rate of the forwards reaction is equal to the rate of the backwards reaction and the concentrations of the reactants and products are constant. Dynamic equilibrium is reached in the following reaction:
$$ N_{2}O_{4(g)} \rightleftharpoons 2NO_{2(g)} $$
- Initially there is a high concentration of dinitrogen tetroxide ($N_{2}O_{4(g)}$) and a low concentration of nitrogen dioxide ($NO_{2(g)}$) so the forwards reaction is fast.
- As more $NO_{2}$ is produced, the molecules start to combine and the rate of the backwards reaction increases.
- Eventually when the rate of the forwards reaction is equal to the rate of the backwards reaction, a dynamic equilibrium is reached.
The concentration-time graph below shows the progress of the reaction.
Equilibrium Law
The equilibrium law shows the relative proportions of reactants and products present at equilibrium. A general reaction can be written as:
$$ aA + bB \rightleftharpoons cC + dD $$
This will have equilibrium concentrations of $[A]$, $[B]$, $[C]$ and $[D]$ for the reactants and products. The equilibrium law states that:
$$ K_{c} = \frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} $$
Where $K_{c}$ is a constant known as the equilibrium constant. For the above reaction in dynamic equilibrium:
$$ N_{2}O_{4(g)} \rightleftharpoons 2NO_{2(g)} $$
The equilibrium constant, $K_{c}$ can be calculated by dividing the concentration of the product, $NO_{2(g)}$ squared by the concentration of the reactant $N_{2}O_{4(g)}$:
$$ K_{c} = \frac{[NO_{2(g)}]^{2}}{[N_{2}O_{4(g)}]} $$
It is important to calculate the correct units for the equilibrium constant. The units for concentration are $mol~dm^{-3}$, which may have to raised to a power depending on the equation.
Homogenous and Heterogeneous Equilibrium
Homogeneous equilibrium: An equilibrium where all the species in the equilibrium are in the same physical state.
Heterogeneous equilibrium: An equilibrium where certain species in the equilibrium are in different physical states.
Calculating Equilibrium Constants
By using experimental results the equilibrium constant of a reaction can be determined. In order to do this, the initial concentrations and concentrations at the time of equilibrium must be known.
Worked Example
$$ H_{2(g)} + I_{2(g)} \rightleftharpoons 2HI_{(g)} $$
$0.60~mol$ of $H_{2(g)}$ was mixed with $0.40~mol$ of $I_{2(g)}$ in a sealed container with a volume of $1.00~dm^{3}$. Once equilibrium was reached, it was found that $0.28~mol$ of $H_{2(g)}$ remained. What is the $K_{c}$?
Component $H_{2(g)}$ $I_{2(g)}$ $2HI_{(g)}$ Initial $0.60$ $0.40$ $0.00$ Equilibrium $0.28$ $0.08$ $0.64$
It is possible to derive this table by using the known molar quantities. As there is a $1:1$ molar ratio between the hydrogen and iodine, when the $H_{2(g)}$ reduces by $0.32~mol$, the $I_{2(g)}$ also reduces by the same amount. As there is a $1:2$ molar ratio between the $H_{2(g)}$ and $HI_{(g)}$ the moles of $HI_{(g)}$ increase by twice the reduction in $H_{2(g)}$.To determine the concentrations from the moles at equilibrium, the number of moles must be divided by the volume. In this case, the volume is $1~dm^{3}$ so the concentrations are equal to the number of moles.
The equilibrium concentraions can then be put into the expression for $K_{c}$. As the units for the concentrations cancel, in this case $K_{c}$ has no units.
$$ \eqalign{
K_{c} &= \frac{[HI_{(g)}]^{2}}{[H_{2}][I_{2}]} \\
K_{c} &= \frac{{0.64}^{2}}{(0.28)(0.08)} \\
K_{c} &= 18.3 \text{ no units}} $$
Equilibrium Position
The magnitude of $K_{c}$ indicates the equilibrium yield of a reaction. The formula for $K_{c}$ is:
$$ K_{c} = \frac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} $$
The products are on the top and the reactants are on the bottom of the fraction. This means that if:
- $K_{c} >> 1$, then the position of equilibrium is towards the right with a high yield of products present at equilibrium.
- $K_{c} << 1$, then the position of equilibrium is towards the left with a high yield of reactants present at equilibrium.
Effect of Temperature on $K_{c}$
Le Chatelier's principle states that an increase in temperature shifts the position of equilibrium in the endothermic direction while a decrease in temperature shifts the position of equilibrium in the exothermic direction. The table below summarises the effect on $K_{c}$ due to changes in temperature:
| Exothermic reaction | Endothermic reaction | |
|---|---|---|
| Temperature Increase | $K_{c}$ decreases | $K_{c}$ increases |
| Temperature Decrease | $K_{c}$ increases | $K_{c}$ decreases |
Effect of Concentrations on $K_{c}$
The value of $K_{c}$ is unchanged by adding or removing products or reactants. If more of a reactant is added to a reaction, the position of equilibrium shifts in order to restore the previous value of $K_{c}$. This results in more product been produced while maintaining the equilibrium constant.
Effect of Catalysts on $K_{c}$
While catalysts affect the rate of reaction, they do not affect the position of equilibrium or $K_{c}$ for a reaction. This is because a catalyst increases both the forwards and backwards rates equally.
Compromises In Industrial Processes
In industrial processes, it is important to find the correct balance between $k$, which determines the rate of reaction and $K_{c}$, which determines the equilibrium yield. For an exothermic reaction such as the Haber Process:
$$ N_{2(g)} + 3H_{2(g)} \rightleftharpoons 2NH_{3(g)} \hspace2ex \Delta H = -92 kJ\,mol^{-1} $$
- At a low temperature, the rate of reaction is slow but as the forwards reaction is exothermic, the equilibrium yield is high.
- At a high temperature, the rate of reaction is fast but as the position of equilibrium would shift in the endothermic direction, the equilibrium yield would be low.