Rates of Reaction
Rate
The rate of reaction is defined as the change in concentration of a reactant or product per unit of time. The units for rate of reaction are $mol~dm^{-3}s^{-1}$.
$$ \text{rate} = \frac{\text{change in concentration}}{\text{time}} $$
The rate depends on many factors including the presence of a catalyst, the temperature and concentrations of the products and reactants. Concentration can be represented by square brackets, so $[CO_{2}]$ refers to the concentration of carbon dioxide.
During a reaction the concentrations of the reactants decrease, so fewer collisions occur per second and the rate decreases. On a concentration-time graph, the rate of reaction can be determined by finding the gradient of the curve. This can be done by plotting a tangent to the curve at a specific point and calculating the gradient of the tangent.
Order
The greater the concentration of the reactants, the greater the number of collisions per second and the greater the rate of reaction. How the concentration of each reactant affects the rate is called the order. There are three common orders:
Zero order: $rate \propto [A]^{0} $. The rate is unaffected by changes to the concentration as any number to the power zero is one.
First order: $ rate \propto [A]^{1} $. If $[A]$ is doubled then the rate of reaction also doubles.
Second order: $rate \propto [A]^{2} $. If $[A]$ is doubled, the rate increases by $2^{2} = 4~\text{times}$.
Rate Equation
The rate equation shows the relationship between the rate of reaction and the concentrations of the reactants raised to the power of their orders. The orders can only be determined from experimental results.
$$ \text{rate} = k[B]^{1}[C]^{2} $$
$k$ is the rate constant which links the rate of reaction with the concentrations of the reactants. A fast reaction has a large value of $k$, while a slow reaction has a smaller value of $k$. The overall order of the reaction is the sum of the individual orders. In the example above the overall order is $1+2=3$.
Units of Rate Constant
The units of $k$ depend on the overall order of the rate equation. The units must balance out the rate equation. The units of rate are $mol~dm^{-3}s^{-1}$ and the units of concentration are $mol~dm^{-3}$. An example for a second order rate equation is shown below:
$$ rate = k[A]^{2} \\ k = \frac{rate}{[A]^{2}} \\ k = \frac{moldm^{-3}s^{-1}}{(moldm^{-3})^{2}} \\ k = dm^{3}mol^{-1}s^{-1} $$
Half Lives
The concentration of a reactant can be measured at time intervals during the course of a reaction. By measuring the change in concentration, a concentration-time graph can then be plotted.
Half Life
The half life of a reactant is the time taken for the concentration of a reactant to reduce by half of its original value.
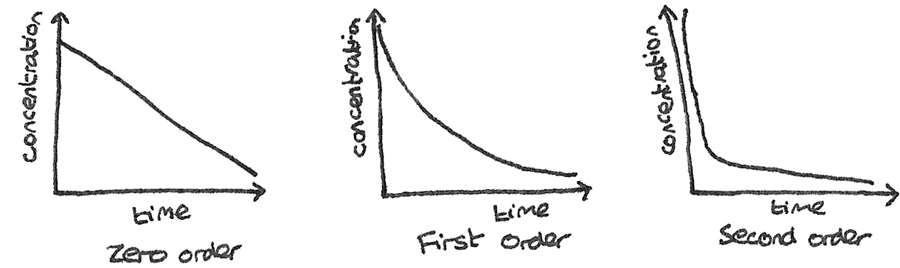
By plotting the a concentration-time graph for a reaction, the order of the reaction can be determined.
- Zero order: The concentration decreases at a constant rate, while the half life decreases with time.
- First order: The concentration halves in equal time intervals, therefore the half life is constant.
- Second order: The concentration decreases rapidly, before the rate of decrease then slows down. The half life increases over time.
Rate-Concentration
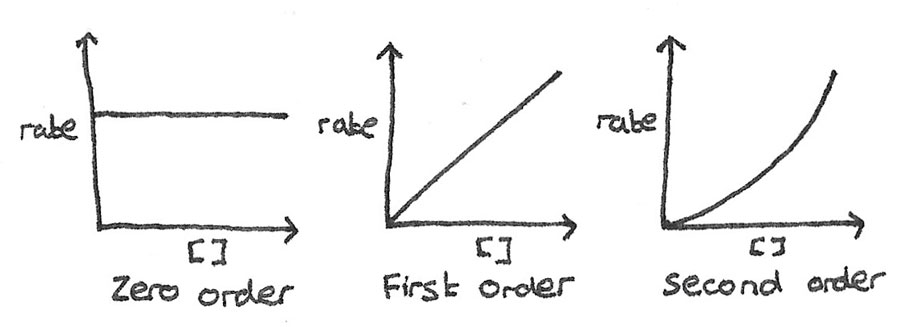
The order can also be determined by plotting a rate-concentration graph.
- Zero order: The rate is unaffected by changes to the concentration.
- First order: The rate is directly proportional to the concentration.
- Second order: The rate increases by a factor of the concentration squared.
Initial Rates
The initial rate can be calculated by finding the gradient of the curve at $t=0$ on a concentration-time graph. This can be done by plotting and calculating the gradient of a tangent.
Alternatively, for clock reactions where there is a visual change the initial rate is proportional to $\frac{1}{t}$, where $t$ is the time taken for the change to occur. Examples of such visual changes include the formation of a precipitate, a colour change or the disappearance of a solid.
Comparing concentrations
It is possible to find the order with respect to each reactant by comparing how the rate changes with changes to the concentration.
Worked Example
Nitrogen dioxide is a pollutant generated in the reaction:
$$ 2NO_{(g)} + O_{2(g)} \rightarrow 2NO_{2(g)} $$
The initial concentrations ($mol~dm^{-3}$) along with the rates ($mol~dm^{-3}s^{-1}$) are shown from three separate experiments.
| Experiment | $[NO]$ | $[O_{2}]$ | Initial rate |
|---|---|---|---|
| 1 | $0.001$ | $0.001$ | $1.82 \times 10^{-6}$ |
| 2 | $0.001$ | $0.003$ | $5.46 \times 10^{-6}$ |
| 3 | $0.002$ | $0.001$ | $7.28 \times 10^{-6}$ |
By comparing experiments 1 and 2, it can be seen that $[NO]$ is constant and $[O_{2}]$ has increased by three times along with the rate. This shows that the order with respect to $O_{2}$ is 1.
By comparing experiments 1 and 3, it can be seen that $[O_{2}]$ is constant and $[NO]$ has increased two times while the rate has increased by a factor of $2^2 = 4$. This shows that the order with respect to $NO$ is 2.
Using these orders along with the information in the table, the rate equation and the rate constant can be determined.
Rate Determining Step
A chemical reaction often occurs in a number of steps, which is called the reaction mechanism. A multi step reaction has a slow step, which determines the overall rate of the reaction. This is the rate determining step.
Rate Determining Step
The slowest step in the reaction mechanism of a multi-step reaction.
Reaction Mechanisms from Rate Equations
The reaction between nitrogen dioxide ($NO_{2}$) and carbon monoxide ($CO$) forms nitrogen monoxide ($NO$) and carbon dioxide ($CO_{2}$).
$$ NO_{2(g)} + CO_{(g)} \rightarrow NO_{(g)} + CO_{2(g)} $$
The overall reaction does not say anything about the reaction mechanism. Rate experiments can be performed to show the orders of the reactants:
- Second order with respect to $NO_{2}$.
- Zero order with respect to $CO$.
This gives the rate equation: $\text{rate} = k[NO_{2}]^{2}$. The orders of the reactants in the rate equation show how many molecules of each reactant are involved in the rate determining step. As $NO_{2}$ is second order, two molecules are the reactants for the rate determining step.
Worked Example
The reaction between nitrogen dioxide ($NO_{2}$) and carbon monoxide ($CO$) forms nitrogen monoxide ($NO$) and carbon dioxide ($CO_{2}$). Find the completed mechanism.
$$ NO_{2(g)} + CO_{(g)} \rightarrow NO_{(g)} + CO_{2(g)} $$
As it is known that two $NO_{2}$ molecules are the reactants in the rate determining step, the first step can be proposed:
$$ \eqalign {
&\text{1st Step} &NO_{2} + NO_{2} &\rightarrow \\
&\text{2nd Step} & &\rightarrow \\
&\text{Overall equation} \hskip 2em &NO_{2} + CO &\rightarrow NO + CO_{2}
}
$$
- $CO$ and $CO_{2}$ must be involved in the second step as they are involved in the overall equation.
- $NO_{2}$ must be a product of the second step as there is only one molecule of $NO_{2}$ is in the overall reaction.
$$ \eqalign {
&\text{1st Step} &NO_{2} &+~NO_{2} &\rightarrow \\
&\text{2nd Step} & &+~CO &\rightarrow CO_{2} + NO_{2} \\
&\text{Overall equation} \hskip 2em &NO_{2} &+~CO &\rightarrow NO + CO_{2}
}
$$
- By balancing the second step equation, the other reactant in the second step must be $NO_{3}$.
- The products of the first step must be $NO$ and $NO_{3}$.
This gives the completed mechanism:
$$ \eqalign {
&\text{1st Step} &NO_{2} + NO_{2} &\rightarrow NO + NO_{3} \\
&\text{2st Step} &NO_{3} + CO &\rightarrow CO_{2} + NO_{2} \\
&\text{Overall equation} \hskip 2em &NO_{2} + CO_{} &\rightarrow NO + CO_{2}
}
$$
Intermediate
An intermediate is a species formed in one step of a multi step reaction that is used up in a subsequent step and is not seen as either a reactant or a product in the overall reaction. In the reaction above, $NO_{3}$ is the intermediate as it is generated in the first step and is consumed in the second step.