Force and Energy
Newton's First Law of Motion
Objects either remain at rest or in uniform motion unless acted on by a resultant force. This means that any object moving at constant velocity is either acted on by no forces or the forces acting upon it are balanced.
Newton's Second Law of Motion
This states that the force is proportional to the mass multiplied by the acceleration:
$$ F = ma $$
Where $F$ is the force $(N)$, $m$ is the mass $(kg)$ and $a$ is the acceleration $(ms^-{1})$. This equation states that with a larger mass, a greater force is required in order to achieve the same acceleration and the more force applied, the greater the acceleration.
Newton's Third Law of Motion
This states that if an object exerts a certain force on another object, then the other object applies an equal and opposite force.
Weight
Weight is the force of an object under gravity. It is equal to:
$$ W = mg $$
Where $W$ is the weight in newtons, $m$ is the mass measured in kg and $g$ is the gravitational field strength which is $9.81Nkg^{-1}$.
Drag
Drag is a force which opposes the direction of motion of an object. It exists as air resistance for objects travelling through air, or as friction between the wheels and the road. Drag only makes an impact on a object under motion, therefore it is never able to make something move. It converts kinetic energy into heat.
Resolving Forces
Newton's second law can be applied to situations where two forces are acting in opposite directions.
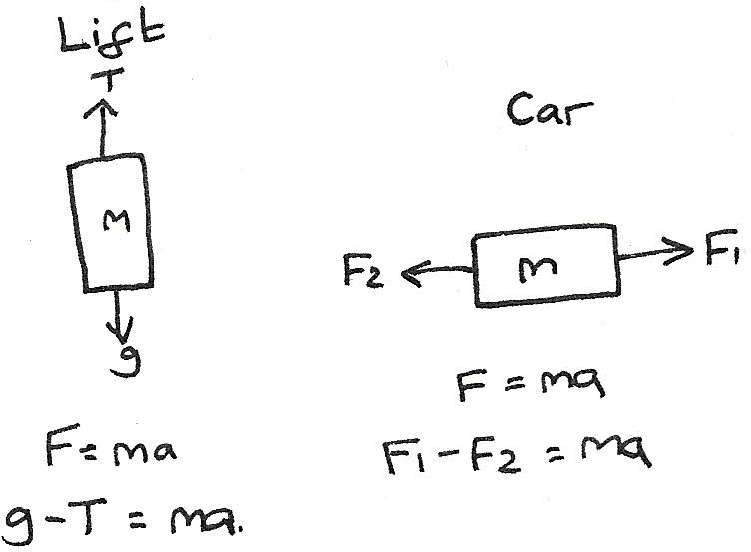
Worked Example
A car of mass 1200kg travelling down a road has a driving force of 200N and undergoes a friction force of 50N. What is the acceleration of the car?
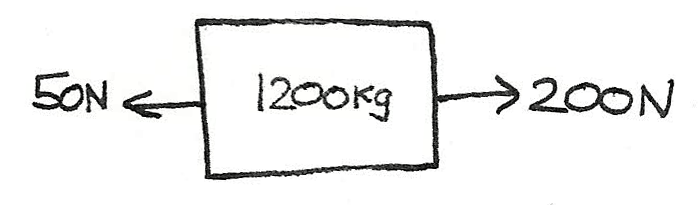
$$ F = ma \\
200 - 50 = 1200a \\
\frac {150}{1200} = a \\
a = 0.125 ms^{-2} $$
Terminal velocity
This is the point at which the forwards force is equal to the frictional force. When this occurs, the acceleration becomes zero as it has reached its maximum speed.
Terminal Velocity for a Car
At first the car accelerates with the driving force far greater than the frictional force. As the velocity increases, the resistance forces increase, reducing its acceleration. The frictional forces will eventually become equal to the driving force meaning it has reached constant velocity.
Terminal Velocity of a Skydiver
- When a skydiver leaves the plane their acceleration increases due to gravity.
- Eventually they will reach terminal velocity where the downwards force is equal to the air resistance.
- To slow the descent, the parachute is opened, increasing the air resistance so that it is greater than the weight.
- This slows the skydiver to a lesser terminal velocity, which is safe enough for landing.
Principle of Conservation of Energy
This principle states that energy cannot be created or destroyed. Instead it is converted between different forms.
Work Done
Work done is the energy converted from one form to another. It can be calculated by:
$$ W = Fd $$
Where $W$ is the work done in joules, $F$ is the force in newtons and $d$ is the distance in metres. On a force-distance graph, the work done can be calculated by finding the area under the curve.
Kinetic Energy
Kinetic Energy is the energy of an object as a result of its motion. It is dependant on the mass of the object and the velocity. It can be calculated by using:
$$ E_{K} = \frac{1}{2}mv^{2} $$
Gravitational Potential Energy
This is the energy due to the position of an object. It can be calculated by using:
$$\Delta E_{P} = mgh $$
Where $\Delta E_{P}$ is the gravitational potential energy in joules, $m$ is the mass in kilograms, $g$ is the gravitational field strength which on Earth is approximately $9.8 ms^{-2} $ and $h$ is the distance vertically above ground.
Energy Changes
If air resistance is ignored when an object is falling, the gravitational potential energy will be equal to the kinetic energy. This is because as the object falls, the potential energy decreases as the kinetic energy increases.
$$ mgh = \frac{1}{2}mv^{2} $$
Power
Power is defined as the rate of energy transfer per second. It is measured in watts ($W$) where 1 watt is equal to the energy transfer rate of 1 joule per second.
$$ P = \frac{\Delta E}{\Delta t} $$
Constant Velocity
For objects travelling at a constant velocity at a constant height, the power is equal to:
$$ P = Fv $$
Where $F$ is the driving force and $v$ is the velocity. This is because the velocity is the distance moved per second and power is defined as the work done per second.
Efficiency
Useful energy is the energy outputted from a system for a certain use. In most systems energy is wasted as it is converted to heat energy through friction. It can be calculated by:
$$ \eqalign{ \text{Efficiency} &= \frac{\text{useful energy transferred}}{\text{energy supplied}} \\
&= \frac{\text{work done}}{\text{energy supplied}}} $$