Waves
Longitudinal Waves
Longitudinal waves are waves in which the direction of vibration of the particles is parallel to the direction of wave travel. In these waves, the particles undergo compression and rarefaction. Examples include seismic and sound waves.
Transverse Waves
Transverse waves are waves in which the direction of vibration of particles is perpendicular to the direction of wave travel. The electromagnetic spectrum is made up of transverse waves.
Plane Polarisation
Only transverse waves can be polarised, meaning that the vibration of particles remain in one plane only. Unpolarised light can be polarised using a polarising filter. By polarising light, the intensity of the light is reduced.
Measuring Waves
- Displacement is the distance and direction from the equilibrium position.
- Amplitude is the maximum displacement of a vibrating particle.
- Wavelength is the least distance between two adjacent vibrating particles in phase.
- One complete cycle is from one maximum displacement to another maximum displacement on a wave.
- The period of a wave is the time taken for one complete cycle to pass a fixed point.
- Frequency is the number of complete cycles of wave passing a fixed point per second. The unit for frequency is hertz (Hz)
$$ \text{period of a wave} = \frac {1}{f} $$
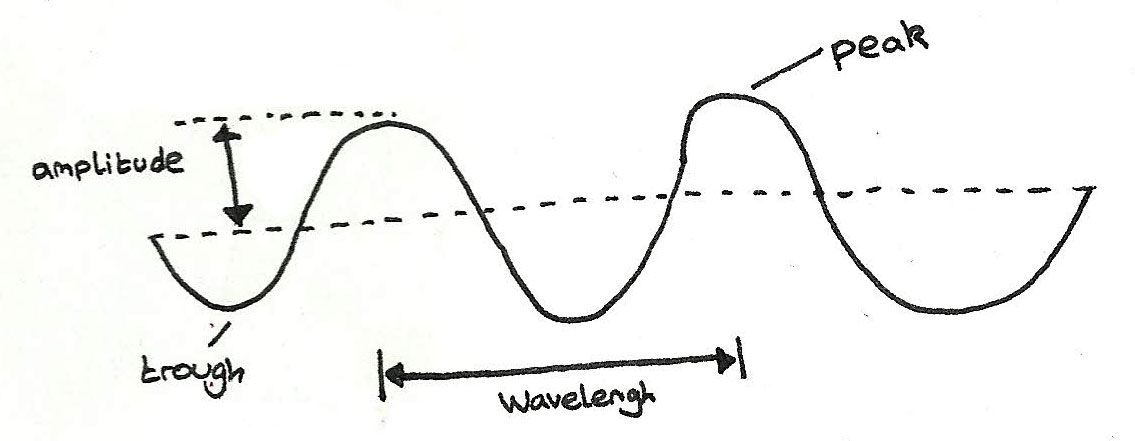
The speed, frequency or wavelength of a wave can be calculated by using the following equation:
$$ c = f\lambda $$
Where $c$ is the speed of the wave, $f$ is the frequency of the wave and $\lambda$ is the wavelength of the wave. This means that as the frequency decreases, the wavelength increases.
Phase Difference
The phase difference between two vibrating particles is the fraction of a cycle between the vibrations of two particles. It can be calculated using:
$$ \text{phase difference} = \frac {2\pi d}{\lambda} $$
Wave Properties
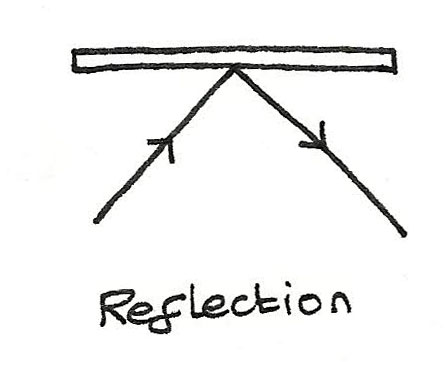
Reflection
When waves are directed above a certain angle at a hard flat surface, the wave reflected has an angle of incidence equal to the angle of reflection.
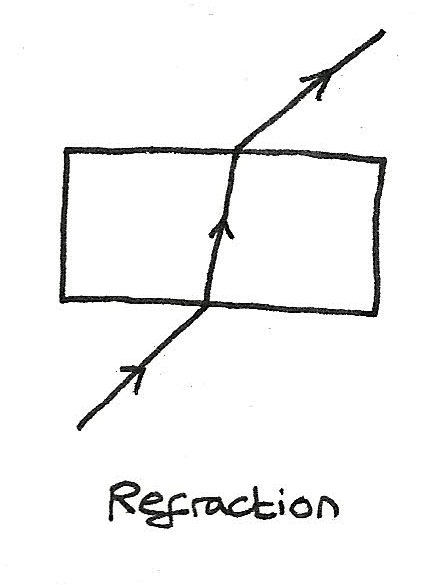
Refraction
When waves pass across a boundary, the wave speed and the wavelength change. If the perpendicular angle of incidence is greater than zero, the light bends which is known as refraction.
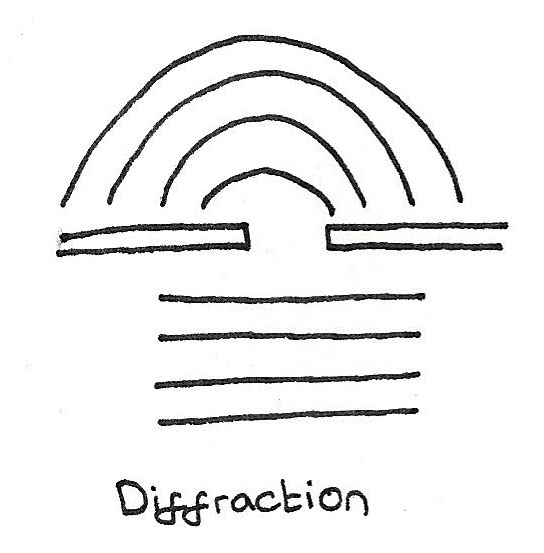
Diffraction
Diffraction occurs when waves spread out after passing through a small gap. The narrower the gap or longer the wavelength, the more the waves spread out.
Superposition
The principle of superposition states that when two waves meet, the total displacement at a point is equal to the sum of the individual displacements at that point.
- When a crest meets a crest, a supercrest is formed. Similarly when a trough meets a trough a supertrough is formed. When this occurs, constructive interference has taken place.
- When a trough meets a crest, destructive interference occurs, where the resultant displacement is zero.
Superposition occurs in ripple tanks where two coherent sources produce waves, forming an interference pattern of constructive and destructive interference.
Coherent Waves
Coherent waves are waves of the same frequency with a constant phase difference.
Stationary Waves
Stationary waves are waves in which some points remain in a fixed position. They are formed when two progressive waves, travelling in opposite directions are in phase which results in destructive interference at nodes (points of no displacement).

| Stationary Waves | Progressive Waves | |
|---|---|---|
| Frequency | All particles except at nodes vibrate at same frequency | All particles vibrate at same frequency |
| Amplitude | Varies from zero to a maximum depending on position | The amplitude is the same for all particles |
| Phase Difference | Equal to $m\pi$ where $m$ is the number of nodes between two particles | Equal to $\frac {2\pi d}{\lambda}$, where $d$ is distance apart and $\lambda$ is wavelength. |
Fundamental Vibration
The fundamental mode of vibration consists of a single loop with a node at each end. For this to occur, the distance between adjacent nodes must be $\frac {1}{2}\lambda$. The fundamental pattern of vibration is the lowest possible frequency. As $L$ is the length between adjacent nodes which is $\frac {1}{2}\lambda$, the fundamental wavelength $\lambda_{0} = 2L$.
The next stationary wave pattern, is where there is a node at the middle. The waves that form this pattern $\lambda_{1} = L$ as each loop forms half a wavelength.
The following stationary wave pattern is the second overtone consisting of three loops. This means the the wavelength $\lambda_{2} = \frac {2}{3}L$