Momentum and Impulse

The momentum of an object is a vector quantity defined as the mass ($kg$) multiplied by the velocity ($ms^{-1}$). Momentum can be expressed in $kgms^{-1}$ or $Ns$.

$$ p = mv $$

According to Newton's second law, the resultant force is directly proportional to the acceleration. As acceleration is the change of velocity over time, it can be shown that the rate of change of momentum of a body is proportional to the net force applied to the body.
$$ F=ma=\frac { m\Delta v }{ \Delta t } =\frac { \Delta mv }{ \Delta t } $$

Conservation of Momentum

The principle of conservation of linear momentum states for a system of interacting objects, the total momentum remains constant, provided no external resultant forces act on the system.

Using the principle of conservation of momentum it is possible to calculate the velocities of colliding objects with known masses:

$$ m_{1}u_{1} + m_{2}u_{2} = m_{1}v_{1} + m_{2}v_{2} $$

Where $m_n$ are the masses, $u_n$ are the initial velocities and $v_n$ are the final velocities.

Worked Example

A fast moving heavy object collides with a slower lighter object. After the collision, the two objects join together.

momentum_collision

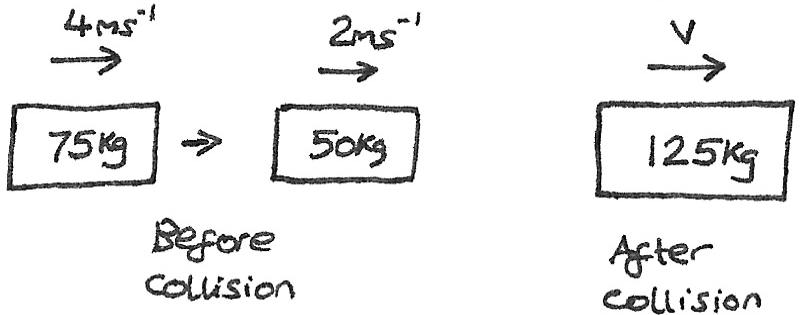
$$ \eqalign{m_{1}u_{1} + m_{2}u_{2} &= m_{1}v_{1} + m_{1}v_{2} \\
75(4) + 50(2) &= 125v \\
400 &= 125v \\
v &= 3.2ms^{-1}} $$

Elastic Collision

An elastic collision is a collision where kinetic energy is conserved.
An inelastic collision is a collision where kinetic energy is not conserved, as some energy is converted into other forms.
A totally inelastic collision is a collision where the colliding objects stick together.

Impulse

The impulse of a collision is defined as the change in momentum. It is a vector quantity. By rearranging Newton's second law, $F=\frac{mv - mu}{t}$, the impulse can be defined as:

$$ Ft = mv - mu $$

Where $Ft$ is the impulse measured in $Ns$, $m$ is the mass of the object, $v$ is the final velocity and $u$ is the initial velocity.

On a force-time graph, the impulse can be determined by calculating the area under the curve.

force_time

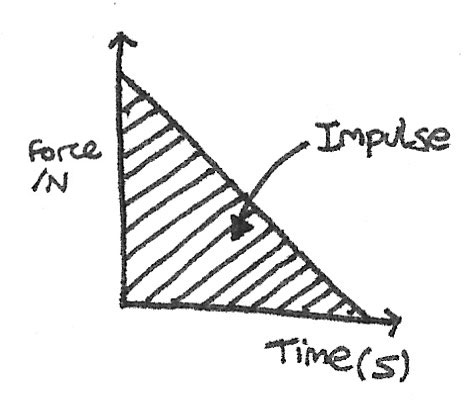
In the impulse equation it can be seen that by increasing the time of a collision, the force applied decreases. This fact is used in car safety, as seat belts and crumple zones are installed to increase the time of a collision, therefore decreasing the applied force.