Circular Motion
Radians
While working with circular motion calculations, it is important to measure angles in radians instead of degrees. Radians are defined as the arc-length divided by the radius of a circle.
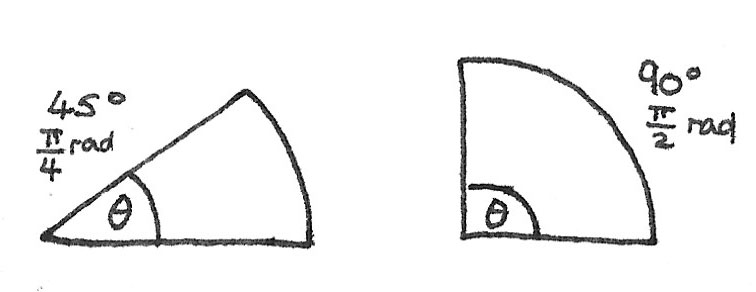
For a complete circle of $360^\circ$, the arc length is $2\pi r$, where $r$ is the radius. Dividing this by a radius of length $1$ gives $2\pi$. This shows that $360^\circ$ is $2\pi$ radians.
Uniform Circular Motion
An object travelling with uniform circular motion is moving with a constant speed in a circular path. The speed of a point on the perimeter can be determined by:
$$ v = \frac{2\pi r}{T} $$
Where $2\pi r$ is the distance around the circumference of a circle and the period $T$ is the time taken for a full revolution.
Angular Displacement
The angular displacement is the angle in radians an object has rotated around a circle, relative to a fixed axis. It can be calculated by:
$$ \theta = \frac{S}{r} $$
Where $\theta$ is the angle in radians, $S$ is the arc length around the circle and $r$ is the radius of the circle.
Angular Velocity
The angular velocity $\omega$, is defined as the angular displacement per second. It can be calculated by using the time taken for a complete revolution:
$$ \omega = \frac{2\pi}{T} $$
As the frequency, $f = \frac{1}{T}$, the angular velocity can also be calculated using:
$$ \omega = 2\pi f $$
The unit of $\omega$ is radians per second ($rad s^{-1}$)
Centripetal Acceleration
As the direction of an object moving around a circle is continuously changing, the velocity is also changing. This means that the object is accelerating while the speed is constant. As this acceleration is acting towards the centre of the circle, this is called the centripetal acceleration.
For an object moving at a constant speed $v$ in a circle of radius $r$, it can be shown that:
$$ a = \frac{v^{2}}{r} $$
Centripetal Force
A resultant force must act on an object in order to make it travel with a circular path. This force is referred to as the centripetal force as it acts in the same direction as the centripetal acceleration, towards the centre of the circle. The reason for the centripetal force depends on the object:
- For an object swinging on the end of a string, the tension acts as the centripetal force.
- For a satellite orbiting around the Earth, the gravitational force acts as the centripetal force.
Calculating Centripetal Force
Newton's second law states that the force is proportional to the acceleration, or $F=ma$. As $a = \frac{v^{2}}{r} = \omega^{2}r$, it can be shown that:
$$ F = \frac{mv^{2}}{r} = m\omega^{2}r $$