Gravitational Fields
Gravitational Fields
A gravitational field is defined as a region of space around a mass where a nearby object experiences a gravitational force. While every object has a surrounding gravitational field, only gravitational fields produced by large masses produce visible effects.
Field Lines
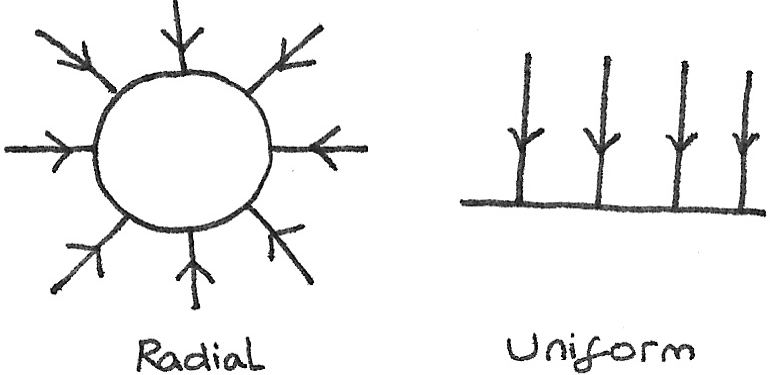
Field lines are the paths that a gravitationally attracted object follows towards a heavier object. There are different types of field patterns:
- Radial Field: This is where the field lines point towards a central point, with the strength of the field decreasing as the distance from the mass increases. All point masses have radial gravitational fields.
- Uniform Field: This is where the field lines are parallel and evenly spaced with an equal gravitational field strength throughout the field. Very close to the surface of any mass, the field lines appear this way.
Newton's Law of Gravitation
Newton's Law of Universal Gravitation states that any two bodies attract each other with a force directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
$$ F = \frac{Gm_{1}m_{2}}{r^{2}} $$
Where $F$ is the force in newtons ($N$), $G$ is the universal constant of gravitation which is $6.67 \times 10^{-11}Nm^{2}kg^{2}$, the $m$ values are the masses of the two objects and $r$ is the distance between the centre of masses of each of the objects.
Gravitational Field Strength
The gravitational field strength, $g$, is the force applied per unit mass on an object placed in a gravitational field. It is a vector quantity and can be calculated with:
$$ g = \frac{F}{m} $$
Where $g$ is has the units $Nkg^{-1}$, $F$ is the gravitational force in newtons and $m$ is the mass. On the surface of Earth, the value of $g$ is $9.8Nkg^{-1}$. It can also be considered as the acceleration under gravity.
By using Newton's Universal Law of Gravitation, the value of $g$ can be calculated, where $M$ is the mass of the large object:
$$ g = \frac{GM}{r^{2}} $$
Gravitational Potential
The gravitational potential, $V$, is the work done per unit mass to move a small object from infinity to that point. The work done ($W$) in order to enable an object with mass $m$ to escape completely is given by $W=mV$. The units of gravitational potential are $Jkg^{-1}$.
$$ V = \frac{-GM}{r} $$
Kepler's Third Law
Kepler's Third Law states that the orbital period of an object is directly proportional to the distance between the objects. It can be derived by using the formulas for centripetal force and gravitational field strength.
$$ T = \sqrt{\frac{4\pi r^{3}}{GM}} $$
Equipotentials
These are lines of constant potential. In the case of a radial gravitational field, these are circular lines of constant gravitational potential around a mass. Along these lines, the gravitational potential energy is constant, therefore no work is done while travelling along a line.
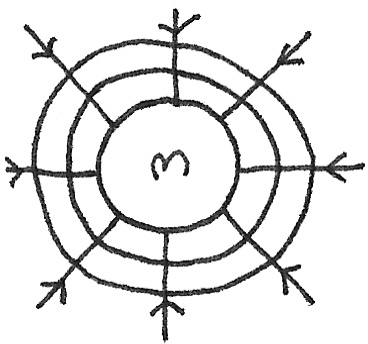
The potential gradient is the change in gravitational potential per metre at that point.
$$ \text{potential gradient} = - \frac{\Delta V}{\Delta r} $$
The difference in gravitational potential between two points can be calculated by using:
$$ \Delta V = -GM ( \frac{1}{R}-\frac{1}{r}) $$
Satellite Motion
Geostationary Satellites
A geostationary satellite orbits the Earth directly above the equator and has a time period of exactly one day. The satellite therefore remains in a fixed position above the Earth. These are useful for communications or weather monitoring.