Simple Harmonic Motion
Oscillations
An oscillating object is an object with a repeating periodic motion between a maximum and a minimum displacement from an equilibrium. Examples of oscillating objects include a spring or a swinging pendulum.
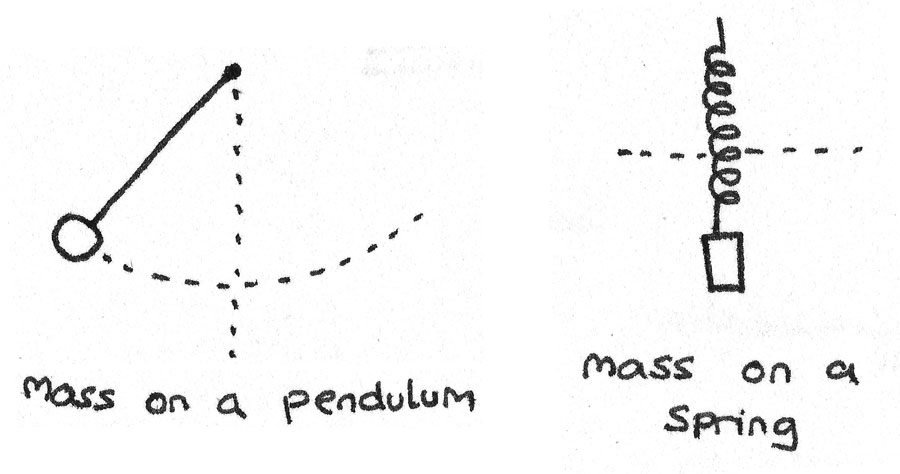
Below are some key terms used to describe the characteristics of an oscillating object:
- Amplitude: The maximum displacement from the equilibrium position.
- Time period: The time taken in seconds for one complete cycle of oscillations. One complete cycle passes when an object travels through the same position in the same direction.
- Frequency: The number of full cycles per second. The frequency can be calculated with $f = \frac {1}{T}$ where $T$ is the time period of the oscillation. The units of frequency are hertz ($\text{Hz}$).
Phase Difference
This is a measure of how “in step” different oscillating objects are. If two objects are at the same position and travelling in the same direction, they are said to be in phase. If not, there exists a phase difference which can be calculated with:
$$ \text{phase difference} = \frac{2\pi\Delta T}{T} $$
Where $T$ is the time period and $\Delta T$ is the time difference between two objects passing the same point in the same direction.
Graphs of Oscillations
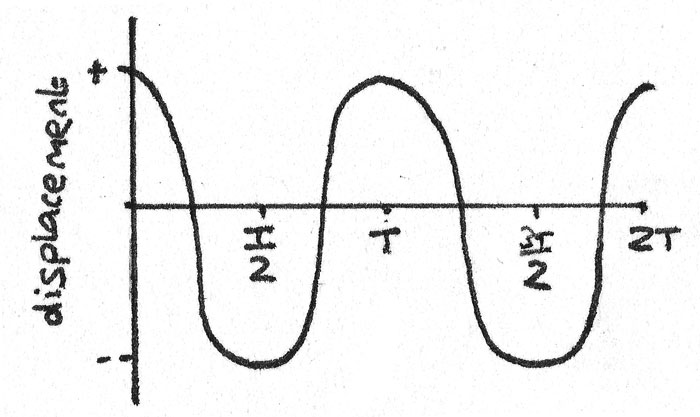
By plotting displacement, velocity and acceleration against time curves, the motion of an oscillating object can be analysed. In the diagrams below, $T$ represents the time taken for one complete cycle of motion.
Displacement against time. The gradient of a displacement-time graph is the velocity of the object.
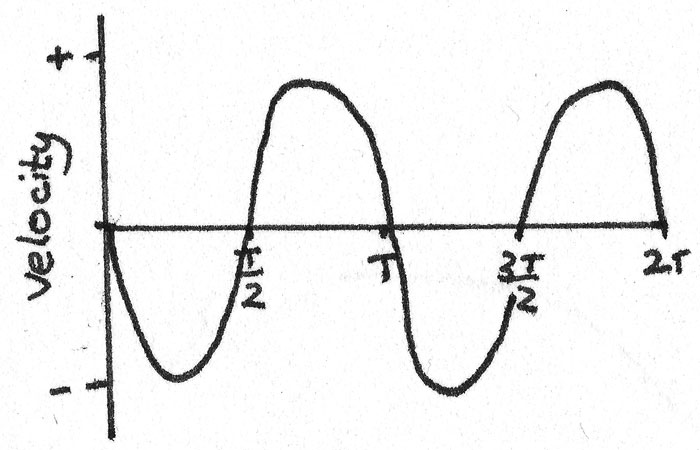
Velocity against time. The gradient of a velocity-time graph is the acceleration of the object.
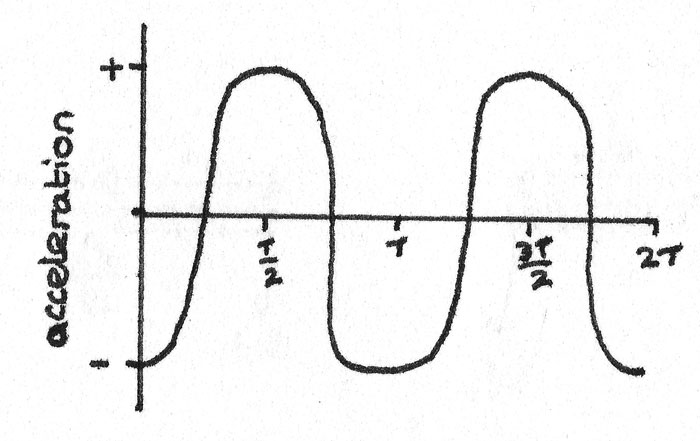
Acceleration against time. The acceleration is zero when the speed is at a maximum.
Simple Harmonic Motion
Simple harmonic motion is defined as an oscillating motion in which the acceleration is proportional to the displacement and is always in the opposite direction to the displacement. The acceleration always acts towards the equilibrium. The acceleration can be calculated with:
$$ a = -(2\pi f)^{2}x $$
Where $a$ is the acceleration ($ms^{-2}$), $f$ is the frequency ($\text{Hz}$) and $x$ is the displacement from the equilibrium position at that point ($m$).
Frequency and Time Period
In simple harmonic motion, the frequency and time period are independent of the amplitude. This means that the time taken for one complete cycle is the same regardless of the initial displacement from equilibrium.
Velocity
The velocity of an object in simple harmonic motion can be found using the formula:
$$ v = \pm 2\pi f \sqrt{A^{2} - x^{2}} $$
Where $v$ is the velocity ($ms^{-1}$), $f$ is the frequency ($\text{Hz}$), $A$ is the amplitude ($m$) and $x$ is the displacement ($m$) from equilibrium at that point.
Sine Curves
The displacement against time graph for an object in simple harmonic motion is a cosine curve. The equation for this curve is therefore:
$$ x = Acos(2\pi ft) $$
Where $x$ is the displacement ($m$), $t$ is the time ($s$), $A$ is the amplitude ($m$) and $f$ is the frequency ($\text{Hz}$). This equation only holds true if at $t=0$ the displacement is at a maximum.
Maximum Acceleration
When the displacement is at a maximum, the acceleration is at a maximum in the opposite direction. This is shown by the equation:
$$ a_{\text{max}} = -(2\pi f)^{2}A $$
Where $a_{\text{max}}$ is the maximum acceleration ($ms^{-2}$), $f$ is the frequency ($\text{Hz}$) and $A$ is the amplitude ($m$) at that point.
Maximum Velocity
By using the formula for the velocity:
$$ v = \pm 2\pi f \sqrt{A^{2} - x^{2}} $$
When the object passes through the equilibrium at $x = 0$, the object is at maximum velocity. This means that the maximum velocity $v_{\text{max}}$ can be calculated with:
$$ v_{\text{max}} = 2\pi f A$$
Where $v_{\text{max}}$ is the maximum velocity ($ms^{-1}$), $f$ is the frequency ($\text{Hz}$) and $A$ is the amplitude ($m$).
Applications of Simple Harmonic Motion
- Mass on a spring. When a mass is pushed or pulled away from equilibrium, a force is applied. Using Hooke’s Law and Newton's second law, it can be stated that:
$$ T = 2\pi\sqrt{\frac{m}{k}} $$
Where $T$ is the time period ($s$), $m$ is the mass of the object ($kg$) and $k$ is the spring constant ($Nm^{-1}$).
- Mass on a pendulum. By using acceleration under gravity along with Newton's second law it can be stated that:
$$ T = 2\pi\sqrt{\frac{l}{g}} $$
Where $T$ is the time period ($s$), $l$ is the length of the pendulum string ($m$) and $g$ is the acceleration under gravity. This equation shows that the mass of the object is independent from the time period.
Free Oscillators
If no external forces act on an oscillator, it is known as a free oscillator. If external forces are applied, the amplitude of oscillations decrease, eventually resulting in the oscillating motion to stop.
As no external forces act on the object, no energy is lost to the surroundings. The total energy of the system is therefore the sum of the kinetic energy, $E_{k}$ and potential energy, $E_{p}$.
$$E_{total} = E_{k} + E_{p}$$
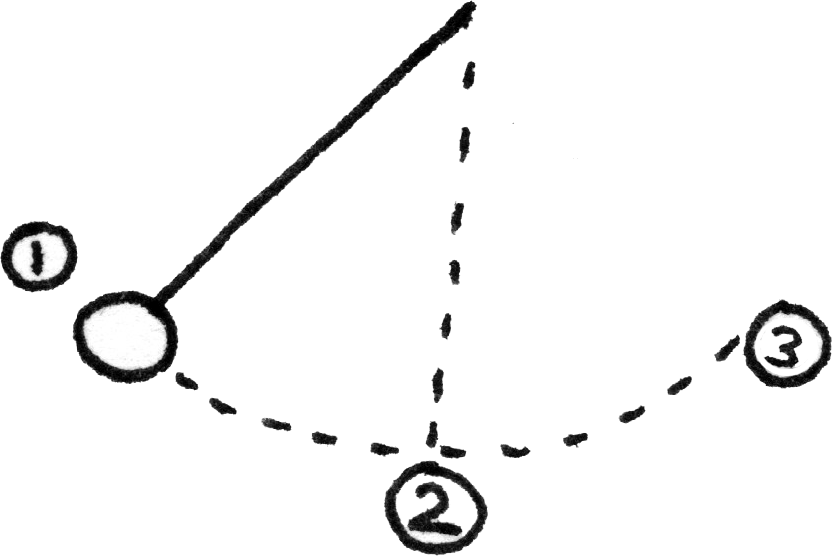
- At maximum displacement, the $E_{p}$ is at a maximum and as the velocity is zero, the $E_{k}$ is zero.
- As the velocity increases towards the equilibrium, the $E_{p}$ is converted into $E_{k}$. At equilibrium where the object is travelling at maximum velocity, the $E_{p}$ is zero and the $E_{k}$ is at a maximum.
- As the oscillating object moves towards the maximum amplitude in the opposite direction, the $E_{k}$ is converted back into $E_{p}$.
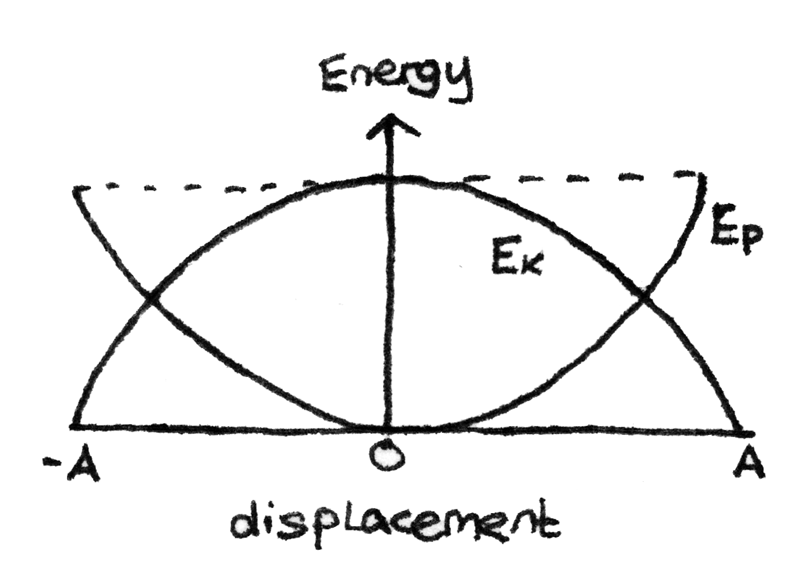
Energy Displacement Curves
The potential and kinetic energy of an oscillating object can be plotted on a graph of energy against displacement. On this graph, the total energy is constant and equal to the potential energy at the maximum displacement.
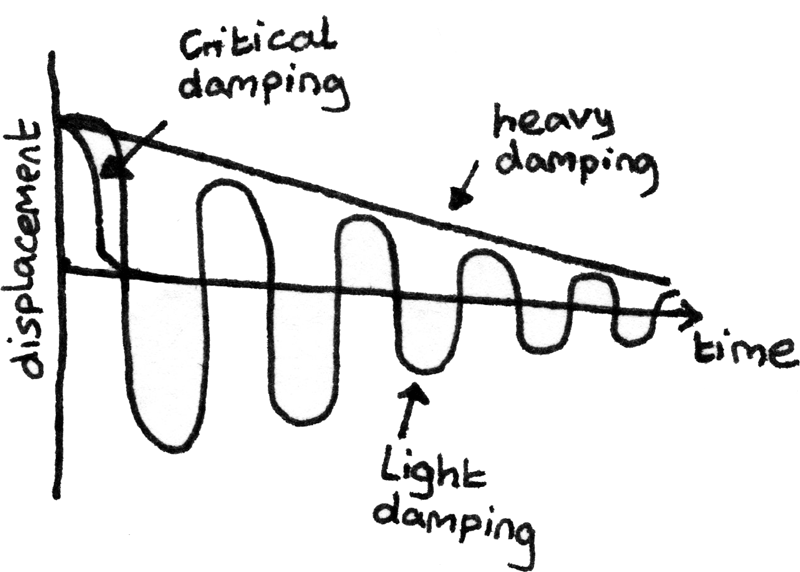
Damping
Damping is where energy in an oscillating system is dissipated to the surroundings resulting in a decreasing amplitude. Damping is caused by dissipative forces such as air resistance or friction.
- Light damping: With light damping, oscillations of constant time period continue with the amplitudes of oscillation gradually decreasing over time.
- Critical damping: With critical damping, the object returns to equilibrium in the shortest possible time without passing through to negative displacement.
- Heavy damping: This is where the resistive forces of damping exceed those of critical damping. This results in the displaced object returning to equilibrium more slowly than if the system was critically damped.
Periodic Force
A force which is applied periodically to an oscillating object is known as a periodic force. When a system oscillates without a periodic force acting on the object, its frequency of oscillation is known as the natural frequency.
When a periodic force is applied to an oscillating system, the system undergoes forced oscillations. The frequency at which the periodic force is applied is known as the applied frequency.
Resonance
When the applied frequency is equal to the natural frequency of the oscillating object, the amplitude of oscillations become very large and the phase difference between the displacement and periodic force is $\frac{\pi}{2}$ radians. At this point the system is resonating. Increasing or reducing the applied frequency results in the amplitude of oscillation decreasing.
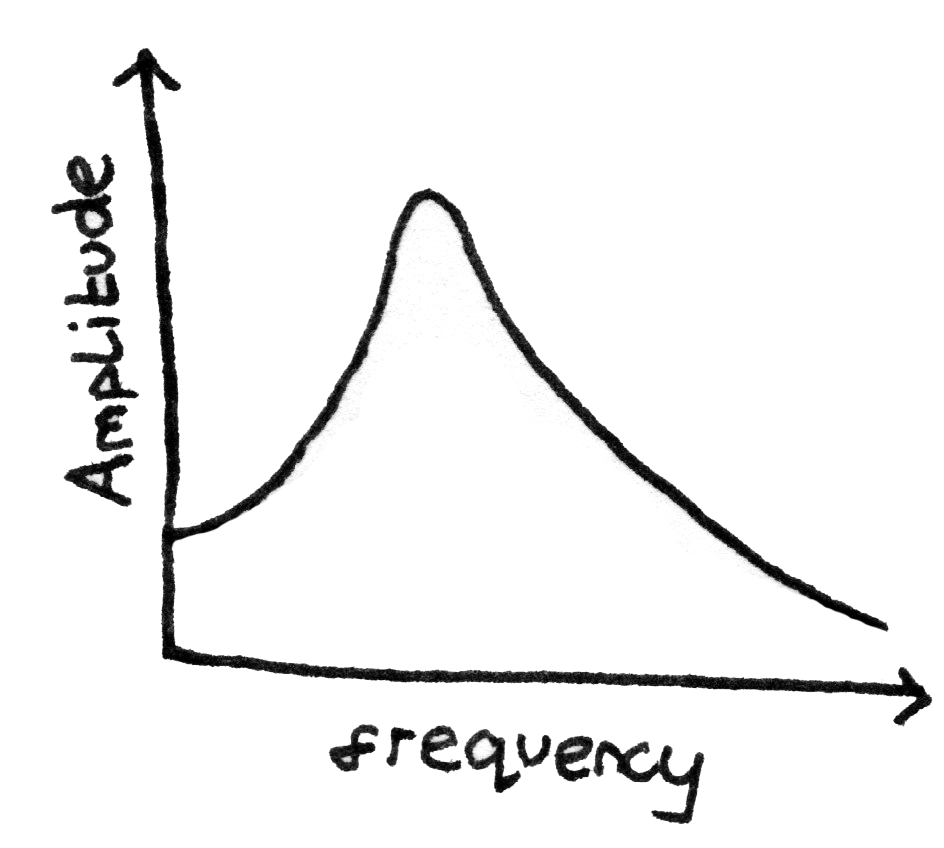
The peak on the graph shows the point where the applied frequency is equal to the natural frequency and the system is resonating.