Electric Fields
Charge
Like charges repel while unlike charges attract. This is due to electrons on the surface of the material. In order to make an object charged, electrons must be added or removed from the surface of a material.
- Electrical conductors – These are materials with an excess of free electrons.
- Insulating materials – These do not contain any free electrons.
Electric Fields
An electric field is a region around a charged particle where a force is exerted on other charged objects. Electric charge $Q$, is measured in coulombs ($C$), and can either be positive or negative.
Field Lines
The path a small positive charge would take in an electric field is called the field line. The direction of the field lines depend on the shape of the objects. The field lines that make up a electric field can take several shapes:
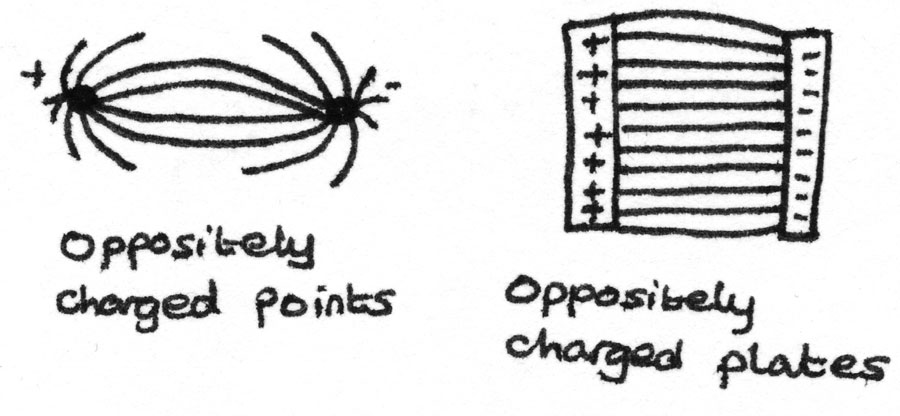
For a uniform field, the field lines are parallel to each other, at right angles to the plates and acting from the positive plate to the negative plate. In a radial field, the field lines point either towards or away from the centre of charge. The stronger the field, the greater the number of field lines per unit area.
Electric Field Strength
The electric field strength, $E$, at a point in a field is defined as the force per unit charge exerted on a positive test charge placed at that point. The unit of $E$ is the newton per coulomb ($NC^{-1}$). This is a vector quantity acting in the direction that the positive charge would move.
$$ E = \frac{F}{Q} $$
Where $F$ is the force in newtons and $Q$ is the charge in coulombs.
Coulomb's Law
Coulomb's Law states that the magnitude of the electrostatic force between two charged objects is directly proportional to the product of the charges and inversely proportional to square of the seperation. A negative force indicates an attractive force and a positive force indicates a repulsive force.
$$ F = \frac{Q_{1}Q_{2}}{4\pi\epsilon_{0}r^{2}} $$
Where $F$ is the force in newtons, $Q_{1}$ and $Q_{2}$ are the charges of the objects, $\epsilon_{0}$ is a constant known as the permittivity of free space and $r$ is the distance between the objects.
Uniform Field
The electric field between two parallel plates produces a uniform field with a constant magnitude and direction of electric field strength. In a uniform field, the electric field strength can be calculated with:
$$ E = \frac{V}{d} $$
Where $V$ is the potential difference in volts, and $d$ is the separation in metres.
Electric Potential
Electric potential is defined as the electrical potential energy per unit charge at a point in a field. It is a scalar quantity and is measured in $JC^{-1}$. It can be calculated using:
$$ V = \frac{W}{Q} $$
The unit of electric potential is volts ($V$). The potential at a point in a field is the work done per coulomb to move a positively charged particle from infinity to that point. It can also be calculated by:
$$ V = \frac{Q}{4\pi\epsilon_{0}r} $$
Where $Q$ is the charge in coulombs, $\epsilon_{0}$ is the permittivity of free space and $r$ is the separation between the centres of the charge.
A graph of the electric potential against distance from the charge can be plotted. The gradient of the graph at a point is the electric field strength. For a uniform field, a straight line is formed as the electric field strength is constant.
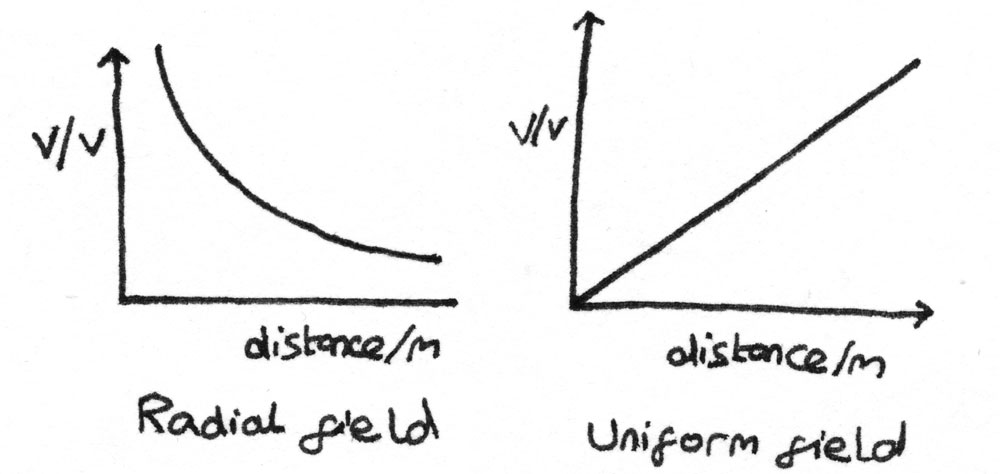
Equipotentials
Equipotentials are points of equal potential within a field. For a uniform field, the equipotentials are equally spaced lines between the plates. In a radial field, these are circular lines with increasing separation as the distance away from the centre increases.
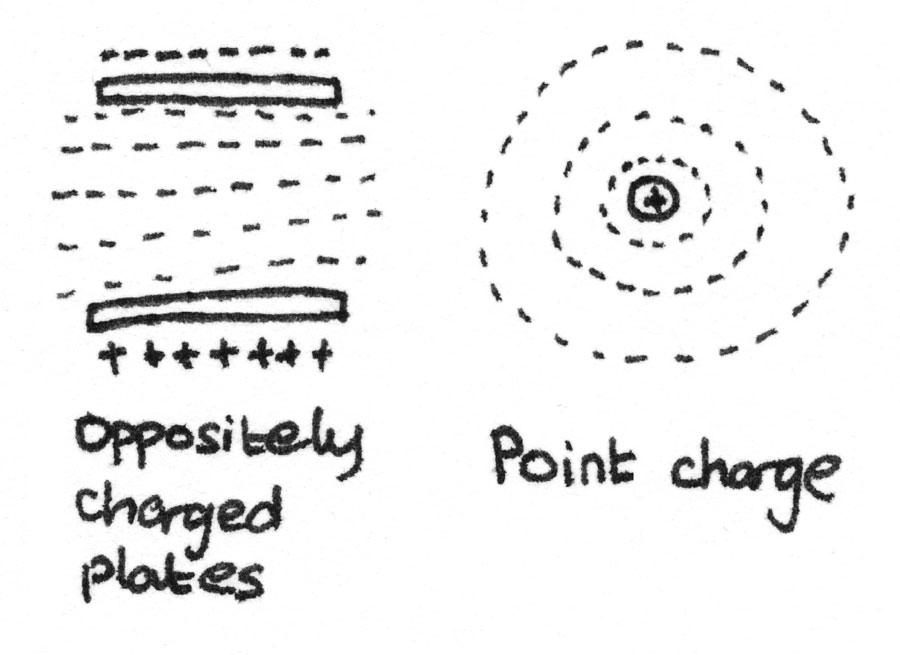
The potential gradient in an electric field is defined as the change in potential per unit distance in a given direction. The electric field strength is equal to negative the potential gradient.