Capacitors

A capacitor is an electrical component used to store electrical charge. Practical uses of capacitors include smoothing out unwanted variations in voltage and as timing control units in timing circuits.

Capacitors consist of two conducting metal plates, separated by an insulating material called a dielectric. When a capacitor is connected to a battery, one plate loses electrons to the battery while the other plate attracts electrons from the battery. This results in a potential difference across the capacitor.

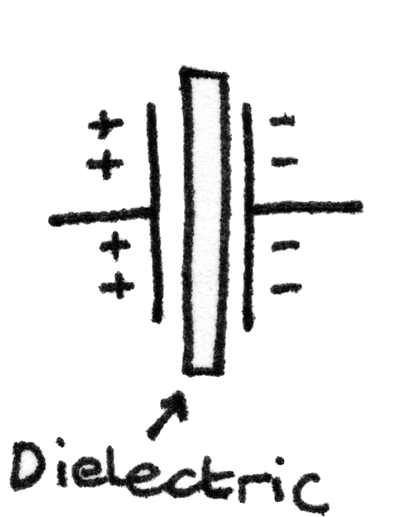
Capacitance

The capacitance, $C$, of a capacitor is defined as the charge per unit potential difference. It can be calculated with:
$$ C = \frac{Q}{V} $$

Where $C$ is the capacitance in farads ($F$), $Q$ is the charge in coulombs ($C$), and $V$ is the voltage in volts ($V$).

Energy Stored

In charging a capacitor, the battery supplies charge $Q$ with a potential difference of $V$ to the circuit. The energy stored can be found by finding the area under a graph of potential difference against charge. This means the energy stored in the capacitor, $E$, can be calculated with:

$$ E = \frac{1}{2}QV $$

Where $Q$ is the charge and $V$ is the voltage across the capacitor. By substituting in the formula $Q = CV$, the equivalent formulae can also be used:

$$ E = \frac{Q^{2}}{2C} = \frac{1}{2}CV^{2} $$

Capacitor Discharge

When the battery is disconnected from the capacitor, the capacitor starts to discharge. The decay of charge follows a negative exponential trend. The equation for the discharge is:

$$ Q = Q_{0}e^{-\frac{t}{RC}} $$

Where $Q$ is the charge in coulombs ($C$) at time $t$, and $RC$ is the time constant. The graph below shows the change in charge over time during the discharge.

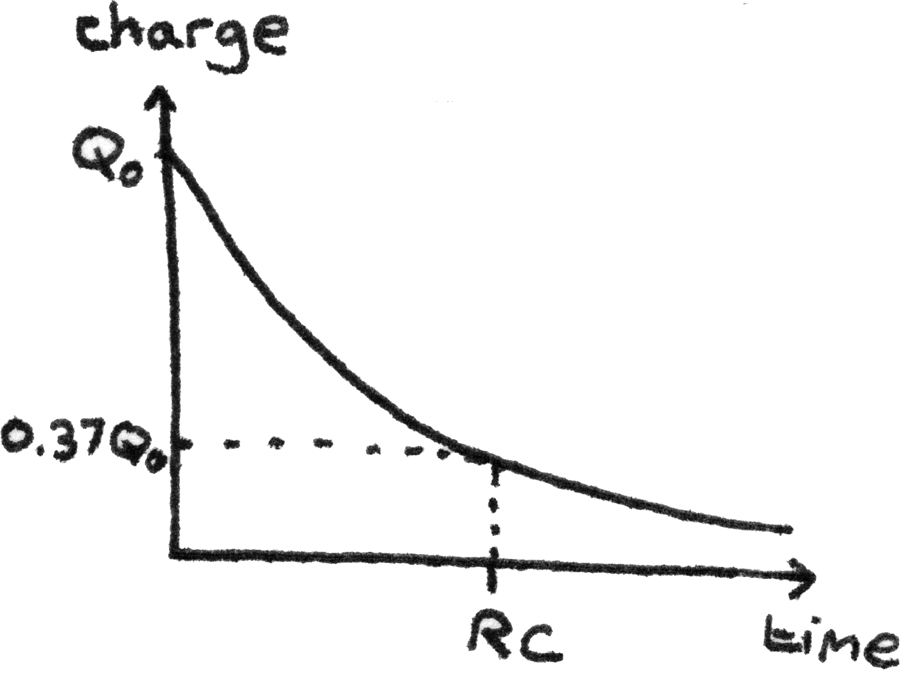
The time constant is the time taken for the charge to fall to $37\%$ of its original value. It can be calculated with:

$$ \text{time constant} = RC $$

Where $R$ is the resistance of the circuit in ohms ($\Omega$) and $C$ is the capacitance in farads ($F$). In circuit design, in order to increase the discharge time the resistance or capacitance could be increased.

Using the formulas $V = IR$ and $Q = CV$, it can be shown that the formula for the decay of current and voltage are similar. This is because the resistance, $R$, and capacitance, $C$, are constants:

$$ I = I_{0}e^{-\frac{t}{RC}} \hspace{25pt} V = V_{0}e^{-\frac{t}{RC}} $$

Capacitor Charging

When a capacitor is connected to a battery, the charge in the capacitor increases until the pd across the capacitor is equal to the source pd. The graph below shows the change in charge over time.

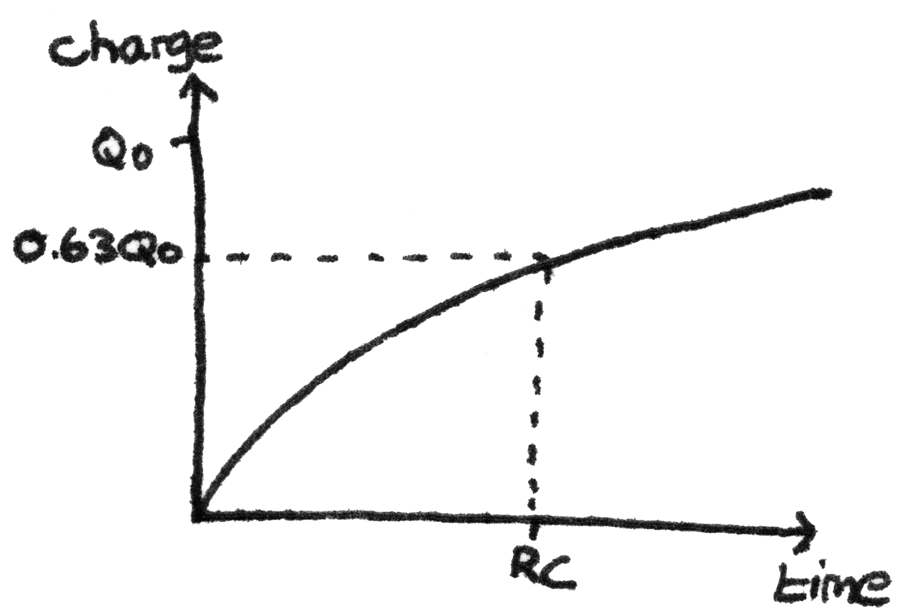
As the current is the change in charge over time, the gradient on this graph is the current. This means that as the charge stored increases, the current decreases. The time constant, $RC$ in charging a capacitor is the time taken for the charge to reach $63\%$ of its final charge.