Engines and Heat Pumps

Engine Cycles

A device which converts heat into useful work is called a heat engine. A heat engine cycles continuously through a series of thermodynamic processes. Two types of engines are shown below.

Four Stroke Petrol Engine

The idealised four stroke petrol engine cycle, also known as the Otto cycle uses a petrol-air mixture as its working substance. The p-V diagram for the cycle is shown below:

petrol_cycle

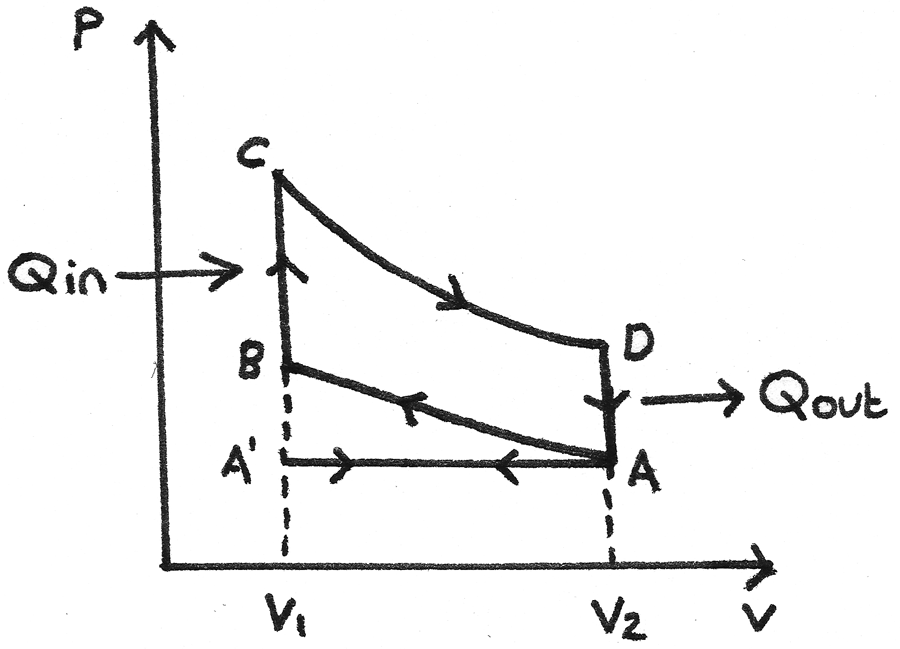
A’ to A - The inlet valve opens which draws in the petrol-air mixture as the piston moves down. This is the induction stroke. At A the inlet valve closes.
A to B - The piston moves up, compressing the gas adiabatically so no heat is transferred. Work is done on the gas. This is the compression stroke.
B to C - At B the spark plug ignites the mixture which increases the pressure rapidly at constant volume. Heat ($Q_{\text{in}}$) is absorbed.
C to D - The gas expands adiabatically, forcing the piston down. The gas does work during expansion. This is the power stroke.
D to A - The gas cools rapidly at constant volume due to contact with the internal walls of the cylinder block. Heat ($Q_{\text{out}}$) is removed.
A to A’ - As the piston moves up, the outlet valve opens and the exhaust fumes are expelled. This is the exhaust stroke.

The net work done by the working substance in one cycle is equal to the
area enclosed by ABCD. This is called an indicator loop.

Idealised Diesel Engine Cycle

The working substance for an idealised diesel engine cycle is diesel fuel. The p-V diagram for this cycle is shown below:

diesel_cycle

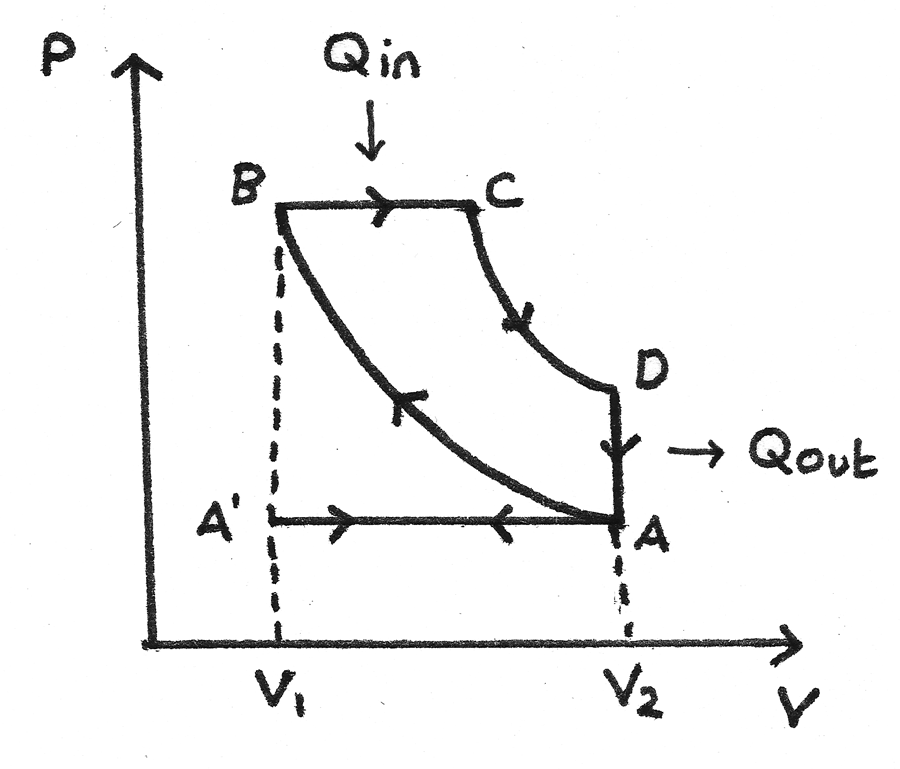
A’ to A - At A’ the inlet valve opens and the exhaust valve closes. Air is drawn into the cylinder at atmospheric pressure as the piston moves down. This is the induction stroke.
A to B - The air is compressed adiabatically causing the temperature to rise. This is the compression stroke.
B to C - Diesel fuel is sprayed into the cylinder and is ignited immediately due to the hot air. This forces the piston down at constant pressure. Heat ($Q_{\text{in}}$) is supplied by the working substance. This is the first part of the power stroke.
C to D - The fuel supply is cut off and the gas expands adiabatically. This is the second part of the power stroke.
D to A - The gas in the cylinder rapidly cools as it comes into contact with the internal walls of the container. The temperature and pressure decrease. Heat ($Q_{\text{out}}$) is released.
A to A’ - The exhaust valve opens and the piston moves up, expelling exhaust fumes. This is the exhaust stroke.

Engine Efficiency

The theoretical efficiency of a petrol engine is around 58% while for a diesel engine it is around 65%. However these theoretical efficiencies are not attained due to frictional effects, turbulence and the composition of air in the chamber.

Compression Ratio

A diesel engine has a higher theoretical efficiency due to a greater compression ratio of $1:20$ compared to $1:9$ for a petrol engine. The compression ratio is the ratio of the volume enclosed in the cylinder at the start of the compression stroke to the end of the stroke.

Real Engine Cycles

The p-V diagrams above represent theoretical engine cycles. In real engines:

There are no sharp changes as the valves take time to open and close.
The expansion and compression strokes are not truly adiabatic as heat transfer will occur.
The maximum temperature may not be reached due to imperfect combustion of the working substance.
The heating and cooling will not occur at constant volume as the piston is constantly moving.

Input Power

The input power of the engine can be given by:
$$ P_{\text{input}} = \text{calorific value of the fuel} (Jkg^{-1}) \times \text{fuel flow rate} (kgs^{-1}) $$
The calorific value is the energy released by the complete combustion of $1kg$ of fuel. The fuel flow rate depends on the state of the engine, how the car is being driven and the type of engine, among other factors.

Indicated Power

The indicated power of an engine is the theoretical capability of the power an engine, if frictionless motion and no unwanted heat transfer is assumed.

$$ P_{\text{ind}} = \text{area of p-V loop} (J) \times \text{number of cycles per second} (s^{-1}) \\ \times \text{number of cylinders} $$

The indicated power can be determined using an indicator diagram, by dividing the net work done by the time taken for one cycle. It is important to note that the power cycle occurs once every two revolutions.

Output Power

The output power or brake power is the power delivered directly to the crankshaft by the engine. It is also referred to as brake horsepower ($bhp$) where $1~bhp = 746W$. It can be calculated with:
$$ P_{\text{out}} = T\omega $$
Where $T$ is the torque ($Nm$) and $\omega$ is the angular velocity ($rad~s^{-1}$).

Frictional Power

As the indicated power is greater than the output power, the difference between the indicated power and the output power is the power loss due to friction in the engine:

$$ P_{\text{friction}} = \text{indicated power} - \text{output (brake) power} = P_{\text{ind}} - P_{\text{out}} $$

Efficiency of an engine

The mechanical efficiency, $\eta$ of an engine can be calculated by dividing the output power by the indicated power.
$$ \eta = \frac{P_{\text{out}}}{P_{\text{ind}}} $$

The thermal efficiency, $\epsilon$ can be calculated by diving the indicated power by the input power.
$$ \epsilon = \frac{P_{\text{ind}}}{P_{\text{input}}} $$

The overall efficiency of an engine can be calculated by finding the product of the mechanical efficiency and thermal efficiency.

$$ \text{overall efficiency} = \eta \times \epsilon = \frac{P_{\text{out}}}{P_{\text{input}}} $$

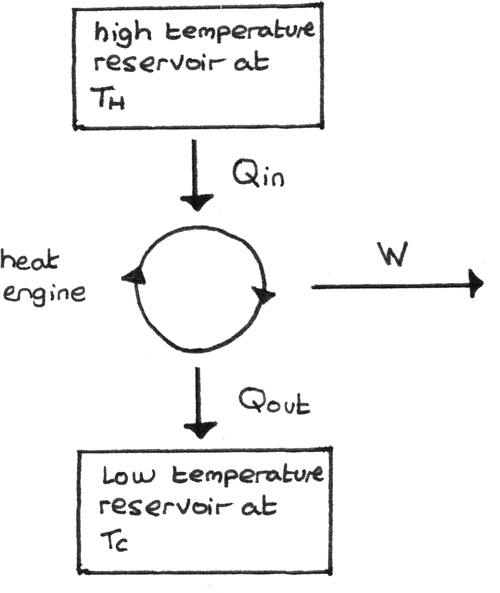
Heat Engines

A heat engine converts heat into useful work. The elements of a heat engine are shown below. Heat ($Q_{\text{in}}$) is taken in from the hot reservoir, work $W$ is done and heat ($Q_{\text{out}}$) is released to the cold reservoir.

heat_engine

Second Law of Thermodynamics

The second law of thermodynamics states that the efficiency of any process for converting heat into work cannot approach $100\%$. This means it is impossible for any heat transfer from a high temperature source to produce an equal amount of work.

For a theoretical engine , $\Delta U = 0$ therefore the work done by the heat engine is given by:
$$ W = Q_{\text{in}} - Q_{\text{out}} $$

A reversible engine is one which can also be operated in reverse. The thermal efficiency of a heat engine can be given by the work done in one cycle divided by the heat transferred from the high temperature source:

$$ \epsilon = \frac{W}{Q_{\text{in}}} $$

As the efficiency depends on the temperature of the high temperature source and the temperature of the low temperature sink:

$$ \frac{T_{H}}{T_{C}} = \frac{Q_{\text{in}}}{Q_{\text{out}}} $$

The maximum theoretical efficiency:
$$ \epsilon_{\text{max}} = \frac{T_{H} - T_{C}}{T_{H}} $$
Where $T_{H}$ is the temperature of the hot reservoir ($K$) and $T_{C}$ is the temperature of the cold reservoir ($K$).

As $T_{H} > T_{C}$, the only theoretical way of achieving a maximum theoretical efficiency of $100\%$ is for $T_{C}$ to be at absolute zero or for $T_{H} \rightarrow \infty$ which are both impossible. In order to maximise the efficiency, the temperature of the source must be high as possible and the temperature of the sink as low as possible.

Reversed Heat Engine

A reversed heat engine is one where the work is done on the working substance such that heat is taken in from the low temperature reservoir and rejected at a higher temperature. The diagram below shows this process:

heat_pump

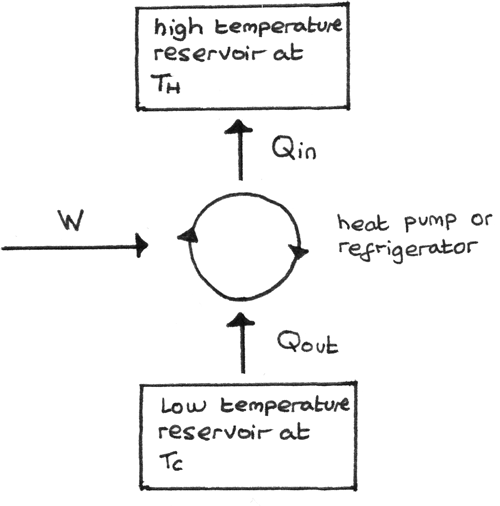
The purpose of a refrigerator is to remove heat from a cold reservoir. This is done by extracting as much energy as possible from the cold reservoir per joule of work done.
The purpose of a heat pump is to supply heat to a hot reservoir. This is done by providing as much energy as possible to the hot reservoir per joule of work done.

Coefficient of Performance

The effectiveness of heat pumps and refrigerators can be measured using a coefficient of performance ($COP$). The $COP$ shows how well a device can transfer work done into heat transfer.

For a refrigerator, as the useful quantity is the $Q_{\text{out}}$:
$$ COP_{\text{ref}} = \frac{Q_{\text{out}}}
{W} =
\frac{Q_{\text{out}}}{Q_{\text{in}} - Q_{\text{out}}} $$

The maxiumum theoretical COP for a refrigerator is given by:
$$ COP_{\text{max}} = \frac{T_{C}}{T_{H} - T_{C}} $$

For a heat pump, as the useful quantity is the $Q_{\text{in}}$:
$$ COP_{\text{hp}} = \frac{Q_{\text{in}}}
{W} =
\frac{Q_{\text{in}}}{Q_{\text{in}} - Q_{\text{out}}} $$

The maxiumum theoretical COP for a heat pump is given by:
$$ COP_{\text{max}} = \frac{T_{H}}{T_{H} - T_{C}} $$

A heat pump and a refrigerator are identical in principle as they both remove heat from a cold reservoir and provide heat to a hot reservoir. Heat pumps provide a low cost and efficient form of heating as the energy pumped into the building for example, is greater than the work done used to drive the compressor.