First Law and p-V Diagrams

The first law of thermodynamics states that the heat energy ($Q$) supplied to a system is equal to the sum of the change in internal energy ($\Delta U$) and the work done ($W$) by the system. It can be represented as:

$$ Q = \Delta U + W $$

A positive $Q$ is a heat transfer into the system and a negative $Q$ is a heat transfer away from a system.
$\Delta U$ is the change in internal energy. For an ideal gas, as the internal energy is due to the kinetic energies of the molecules, the temperature only depends on the internal energy. Therefore an increase in the internal energy of a system results in an increase in temperature of the system.
A positive $W$ is the work done by the system such as during the expansion of a gas and a negative $W$ is the work done on the system such as during the compression of a gas.

All these quantities are expressed in joules ($J$).

Work Done by Ideal Gas

In an ideal gas, no forces of attraction act between gas molecules therefore they possess no molecular potential energy. This means that the temperature depends only on the internal energy ($U$) which in turn depends on the kinetic energy of the molecules.

To change the internal energy of a gas, work must be done or heat transfer must occur. For a tube of gas at pressure $p$ in a piston:

piston_work

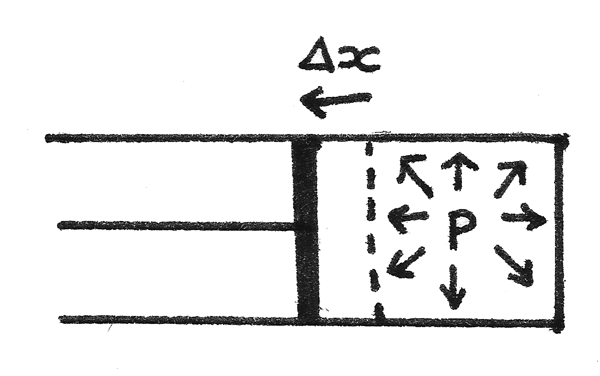
The force applied on the piston by the gas is equal to $pA$ where $A$ is the cross sectional area of the piston.
If the gas is allowed to expand slightly without a significant change in the pressure, the piston will move a distance $\Delta x$. This results in a change in volume equal to $A\Delta x$.
As the work done is equal to the force multiplied by the distance moved:
$$ W = F\Delta x \\
W = pA\Delta x \\
W = p\Delta V $$

Non-Flow Processes

Isothermal Process

An isothermal process is a process that takes place under constant temperature conditions. For an ideal gas, the temperature only depends on the internal energy so $\Delta U = 0$. This results in the heat transfer being equal to the work done:
$$ Q = W $$
In order to maintain a constant temperature when a gas is expanding and doing external work $W$, an equal amount of heat $Q$ must be transferred into the system. For an ideal gas:
$$ pV = \text{constant} $$

Therefore for an isothermal change,
$$ p_{1}V_{1} = p_{2}V_{2} $$
Where $p_{1}$ and $V_{1}$ are the initial pressure ($Pa$) and volume ($m^{3}$) of the gas and $p_{2}$ and $V_{2}$ are the final pressure ($Pa$) and volume ($m^{3}$) of the gas.

Adiabatic Process

An adiabatic process is a process that takes place in such a way that no heat can enter or leave a system. This means that $Q = 0$ so the work done by the system is equal to the loss in internal energy:

$$ W = -\Delta U $$

Therefore if the gas does work, the internal energy decreases and the temperature falls. While a truly adiabatic process is not possible, near adiabatic conditions can be achieved by reducing the volume rapidly or using a very well insulated container.

When an ideal gas undergoes an adiabatic expansion or compression, the adiabatic equation can be used:
$$ pV^{\gamma} = \text{constant} $$
Where $\gamma$ is the adiabatic constant which depends on the molecular structure of the gas. Typical values include $\gamma = 1.67$ for a monatomic gas and $\gamma = 1.40$ for a diatomic gas. For an adiabatic change:

$$ p_{1}V_{1}^{\gamma} = p_{2}V_{2}^{\gamma} $$
Where $p_{1}$ and $V_{1}$ are the initial pressure ($Pa$) and volume ($m^{3}$) of the gas and $p_{2}$ and $V_{2}$ are the final pressure ($Pa$) and volume ($m^{3}$) of the gas.

The ideal gas equation can also be used in order to determine the initial or final temperatures:

$$ \frac{p_{1}V_{1}}{T_{1}} = \frac{p_{2}V_{2}}{T_{2}} $$
Where $T_{1}$ is the initial temperature ($K$) and $T_{2}$ is the final temperature ($K$).

Constant-Volume Process

This is a process where the volume is held constant, such as the heating of a gas in a rigid fixed container. If the volume is constant no work can be done so $W = 0$. This means that the heat transfer is equal to the change in internal energy:
$$ \Delta U = Q $$

If heat is absorbed into a system, the internal energy of the system rises.

Constant-Pressure Process

This is a process where the pressure is held constant, such as when a gas is heated in a cylinder with a movable frictionless piston. As the work done is equal to the pressure multiplied by the change in volume:

$$ W = p\Delta V $$

The first law of thermodynamics can then show that the heat energy supplied to a system is equal to the sum of the change in internal energy and the product of the pressure and change in volume:
$$ Q = \Delta U + p\Delta V $$

P-V Diagrams

A pressure-volume diagram, also known as an indicator diagram is used to show changes to the pressure and volume in thermodynamic cycles. The area under a p-V curve represents the work done on or by a gas. Some p-V diagrams are shown below:

Constant Pressure and Constant Volume

constant_volume_pressure

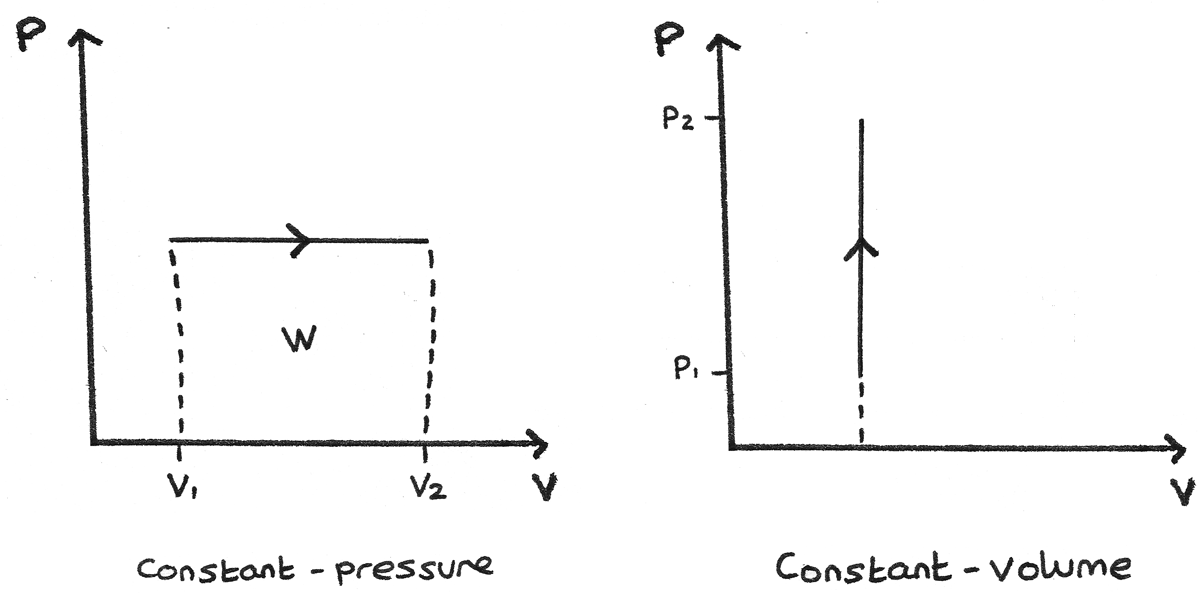
A constant pressure process is represented as a horizontal line. The work done is the area under this line. If the volume is increasing through expansion, the work is done by the gas. If the arrow is reversed and the volume is decreasing, work is done on the gas.
A constant volume process is represented as a vertical line. As in a constant volume process no work can be done, the area under this curve is zero.

Thermodynamic Cycle

p-V diagrams can be used to show closed thermodynamic cycles whereby a system is taken back to its original state.

thermodynamic_cycle

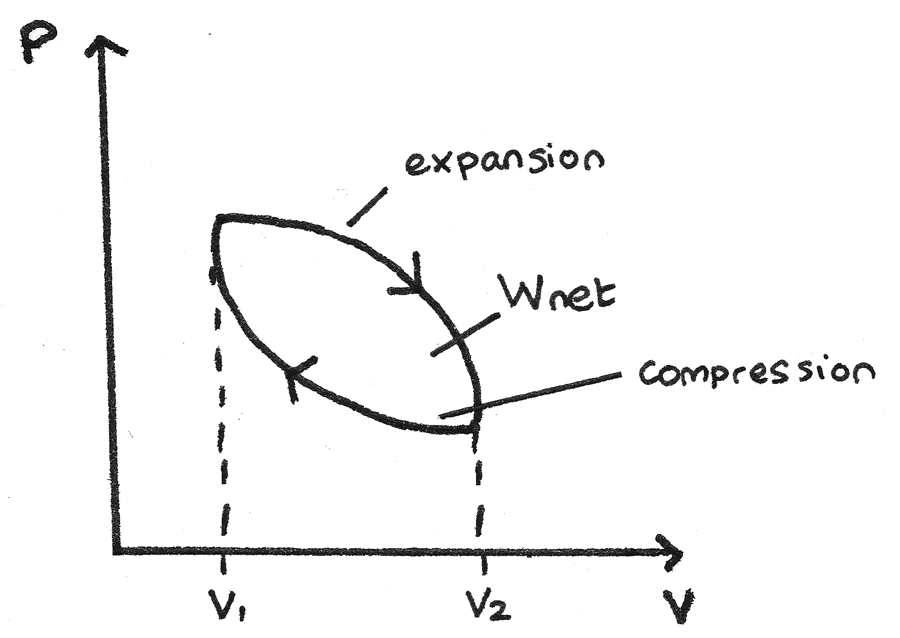
From the high pressure to high volume, the gas expands so the area under the curve is the work done by the gas.
From the high volume to high pressure, the gas is compressed so the area under the curve is the work done on the gas.

Since the area under the expansion curve is greater than the area under the compression curve, the net work done by the gas is positive and is represented by the area between the curves.

Isothermal and Adiabatic Expansions

In an adiabatic process no heat transfer can occur as $\Delta U = 0$, whereas in an isothermal process the temperature is constant. During an isothermal expansion, heat can be transferred to the gas which increases the pressure. This results in the adiabatic expansion having a steeper curve.

isothermal_adiabatic

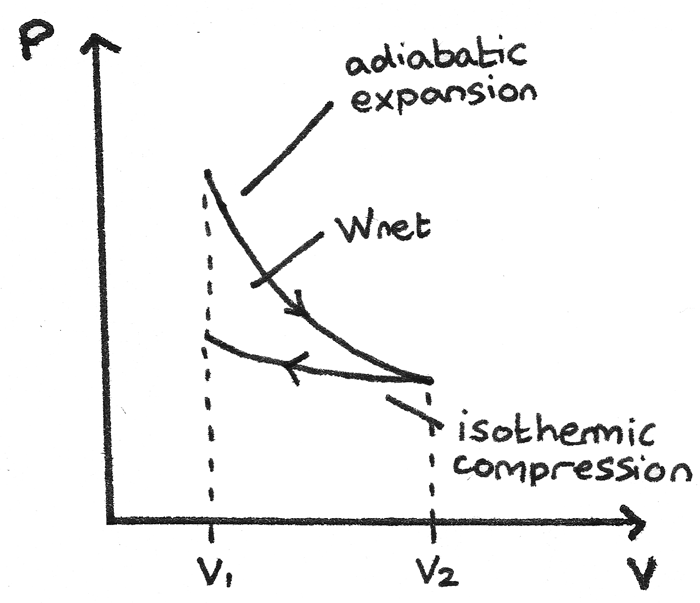
Adiabatic Expansion with Isothermal Compression

This p-V diagram shows a gas that has been expanded adiabatically then compressed isothermally to its original volume. The area between the curves is the net work done by the gas.

adiabatic_isothermal