Rotational Dynamics

Rotational dynamics can be used to describe an object travelling in circular motion while linear dynamics describe an object travelling in a straight line. In rotational dynamics, angles and angular displacements are measured in radians instead of degrees.

Angular Displacement

Angular displacement is the angle an object has rotated around a circle relative to a fixed axis. It can be calculated by:

$$ \theta = \frac{S}{r} $$

Where $\theta$ is the angle in radians, $S$ is the arc length around the circle and $r$ is the radius of the circle.

Angular Velocity

Angular velocity is the angular displacement travelled per second.

$$ \omega = \frac{\Delta{\theta}}{\Delta{t}} $$

Where $\omega$ is the angular velocity ($rad~s^{-1}$), $\theta$ is the angular displacement ($rad$) and $t$ is the time ($s$). It can also be calculated using the time period $T$ of a rotation:
$$ \omega = \frac{2\pi}{T} $$

An increase in the angular velocity results in an increase in the linear velocity:
$$ v = r \omega $$
Where $v$ is the linear velocity ($ms^{-1}$), $r$ is the radius of the circle ($m$) and $\omega$ is the angular velocity ($rad~s^{-1}$).

Angular Acceleration

Angular acceleration is the rate of change of angular velocity.

$$ \alpha = \frac{\Delta{\omega}}{\Delta{t}} $$

Where $\alpha $ is the angular acceleration ($rad~s^{-2}$), $\omega $ is the angular velocity ($rad~s^{-1}$) and $t$ is the time ($s$). An increase in the angular acceleration results in an increase in the linear acceleration:
$$ a = r\alpha $$
Where $a$ is the linear acceleration ($ms^{-2}$), $r$ is the radius of the circle ($m$) and $\alpha$ is the angular acceleration ($rad~s^{-2}$).

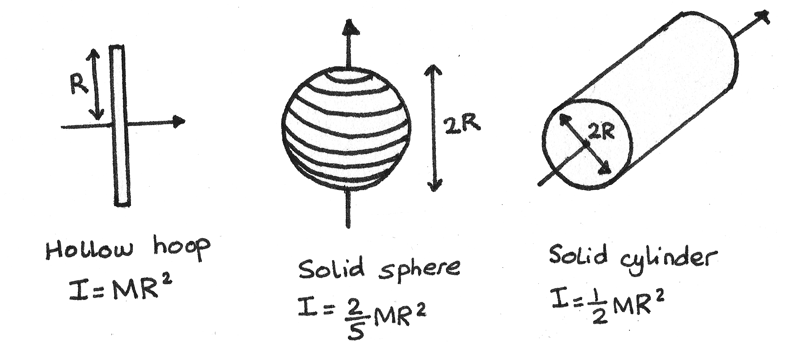
Moment of Inertia

The dynamics of a rotating object depend on the distribution of mass relative to a particular axis of rotation. An object can be considered as being made up of an infinite number of point masses of mass $m_{i}$ each a distance $r_{i}$ away from a central axis.

The rotational kinetic energy of a single point mass will therefore be:
$$\frac{1}{2}m_{1}v_{1}^{2} = \frac{1}{2}m_{1}{(\omega r_{1})}^{2} = \frac{1}{2}\omega^{2} m_{1}r_{1}^{2} $$

Adding together all the individual kinetic energies gives the total kinetic energy of the object:

$$ E_{k} = \frac{1}{2}\omega^{2} m_{1}r_{1}^{2} + \frac{1}{2}\omega^{2} m_{2}r_{2}^{2} + \cdots + \frac{1}{2}\omega^{2} m_{i}r_{i}^{2} $$

As the angular velocity $\omega$ is equal for all of the point masses:
$$ \eqalign{ E_{k} &= \frac{1}{2}\omega^{2}(m_{1}r_{1}^{2} + m_{2}r_{2}^{2} + \cdots + m_{i}r_{i}^{2}) \\
E_{k} &= \frac{1}{2}\omega^{2}(\Sigma m_{i}r_{i}^{2})} $$

The $\Sigma m_{i}r_{i}^{2}$ term is defined as the moment of inertia, which is a measure of the resistance of an object to an angular acceleration.

$$ I = \Sigma m_{i}r_{i}^{2} $$

The units of $I$ are $kg~m^{2}$. Different shaped objects have different expressions for the moment of inertia.

moment_inertia
If two objects share a common axis of rotation, the sum of the moments of inertia gives the combined moment of inertia for the system. For two flywheels of moments of inertia $\frac{1}{2}M_{A}R_{A}^{2}$ and $\frac{1}{2}M_{B}R_{B}^{2}$, the total moment of inertia of the system is:
$$ I = \frac{1}{2}M_{A}R_{A}^{2} + \frac{1}{2}M_{B}R_{B}^{2} $$

Rotational Kinetic Energy

As shown above, the rotational kinetic energy of an object rotating around a given axis is:

$$ \eqalign{ E_{k} &= \frac{1}{2}\omega^{2}(\Sigma m_{i}r_{i}^{2}) \\
E_{k} &= \frac{1}{2}I\omega^{2} }$$

Where $E_{k}$ is the rotational kinetic energy ($J$), $I$ is the moment of inertia ($kgm^{2}$) and $\omega$ is the angular velocity ($rad~s^{-1}$). It is important to ensure that the rotational velocity is converted from $rev~min^{-1}$ to $rad~s^{-1}$.

Flywheels

Flywheels are used to store rotational kinetic energy. Some uses of flywheels are shown below:

Factors Affecting Energy Store

The maximum energy store of a flywheel is given by the maximum rotational kinetic energy of the flywheel:

$$ E_{k} = \frac{1}{2}I\omega^{2} = \frac{1}{2}\omega^{2}(\Sigma m_{i}r_{i}^{2}) $$

This equation shows that the maximum rotational kinetic energy depends on the angular velocity ($\omega$) and the moment of inertia ($I$). The rotational kinetic energy can be increased by:

Equations of Rotational Motion

There are four equations of rotational motion that are similar to the equations of linear motion. The quantities used are shown below:

The equations of rotational motion are shown below:

$$ \eqalign{
\omega_{2} &= \omega_{1} + \alpha t \\
\theta &= \omega_{1} t + \frac{1}{2}\alpha t^{2} \\
\omega_{2}^{2} &= \omega_{1}^{2} + 2\alpha \theta \\
\theta &= \frac{1}{2}(\omega_{1} + \omega_{2})t } $$

Torque

The torque is the product of the force and perpendicular distance of the line of action of the force from a fixed axis.

torque
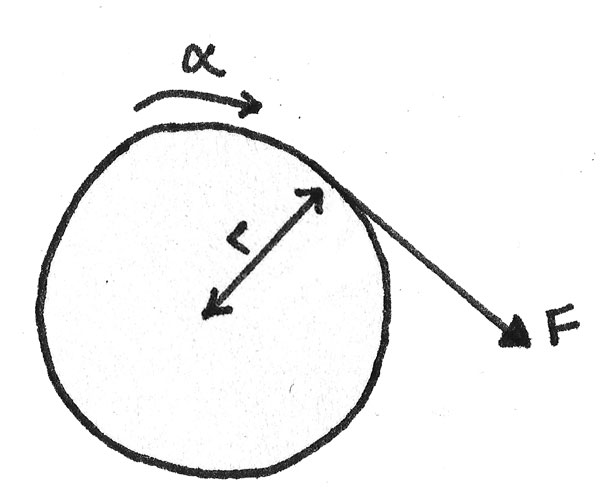
$$ T = Fs $$

Where $T$ is the torque ($Nm$), $F$ is the applied force ($N$) and $s$ is the perpendicular distance ($m$). For most rotating systems, this is the radius of the circle. Using Newton’s second law, the torque can be expressed in terms of the moment of inertia of the object:

$$ T = I\alpha $$

Where $T$ is the torque ($Nm$), $I$ is the moment of inertia ($kgm^{2}$) and $\alpha$ is the angular acceleration ($rad~s^{-2}$).

Angular Momentum

The angular momentum of a rotating object is a vector quantity acting parallel to the angular velocity defined as:
$$ L = I\omega $$
Where $L$ is the angular momentum ($Nms$), $I$ is the moment of inertia ($kgm^{2}$) and $\omega$ is the angular velocity ($rad~s^{-1}$).

Likewise to linear momentum, the conservation of angular momentum states that when no external torque acts on a closed system, the total angular momentum remains constant.

This means that if the moment of inertia $I$ increases by concentrating an object’s mass at a greater distance from the central axis, the angular velocity of the object must decrease to keep the angular momentum constant. An example of this is a dancer extending their arms while rotating in order to slow themselves down.

A clutch is another example of the conservation of angular momentum in action:

clutch

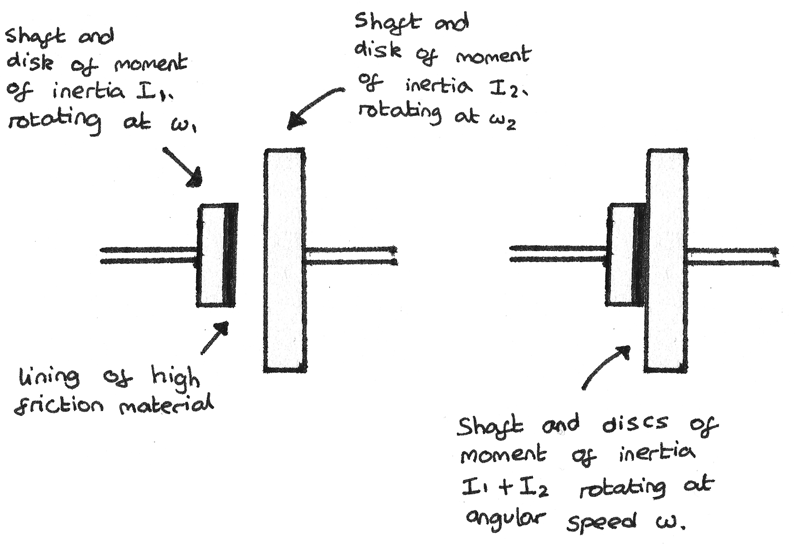
Before the engagement, the total angular momentum is:
$$ L_{\text{before}} = I_{1}\omega_{1} + I_{2}\omega_{2} $$
After the engagement, the total angular momentum is:
$$ L_{\text{after}} = (I_{1} + I_{2})\omega_{2} $$
Due to the conservation of angular momentum:
$$ \eqalign{
L_{\text{before}} &= L_{\text{after}} \\
I_{1}\omega_{1} + I_{2}\omega_{2} &= (I_{1} + I_{2})\omega} $$

Angular Impulse

An angular impulse, $\Delta L$ is a change in angular momentum, $L$.

$$ \Delta L = I\omega_{2} - I\omega_{1} $$
Where $\Delta L$ is the change in momentum ($Nms$), $I$ is the moment of inertia ($kgm^{2}$), $\omega_{1}$ is the angular velocity ($rad~s^{-1}$) before the change in momentum and $\omega_{2}$ is the angular velocity ($rad~s^{-1}$) after the change in momentum.

When the moment of inertia is constant, an angular impulse can be related to torque by the expression:

$$ T = I\alpha = I\frac{\Delta \omega}{\Delta t} = \frac{\Delta L}{\Delta t} \\ \\
\Delta L = T\Delta t $$

This equation shows that the torque acting acting over a time interval is equal to the angular impulse.

Work Done

In rotational dynamics, the work done is the product of the force applied and the angular displacement. For a rotating system, the work done can be defined as:

$$ W = T \theta $$

Where $W$ is the work done ($J$), $T$ is the torque applied ($Nm$), and $\theta$ is the angle the object has rotated through. Work may be done to overcome resistive forces or to increase the angular velocity of the rotating object.

Power

As power is the rate of doing work, it can be defined as:
$$ P = \frac{\Delta W}{\Delta t} = T \frac{\Delta \theta}{\Delta t} $$
Where $\frac{\Delta \theta}{\Delta t}$ is the rate of change of angular displacement. The power can therefore be defined as:
$$ P = T\omega $$
Where $P$ is the power ($W$), $T$ is applied torque ($Nm$) and $\omega$ is the angular velocity ($rad~s^{-1}$).

Return to Physics First Law and p-V Diagrams > >
© Andrew Deniszczyc, 2024