Enthalpy

What is a Chemical Change?

Chemical energy is a special form of potential energy that exists within chemical bonds. When chemicals react, the bonds break in the reactants and new bonds are formed within the products.

Enthalpy

Enthalpy, $H$, is the heat content stored in a chemical system.

Within a chemical system, the law of conversation of energy exists where the amount of energy released is always the same as the energy that goes into the surroundings. This energy change can be measured as heat. These changes of heat can be described as:

Exothermic
This is when heat energy is released to the surroundings, therefore increasing the temperature of the surroundings. This means that the enthalpy of the system decreases giving a negative $\Delta H$.
Endothermic
This is when the energy is taken in from the surroundings, therefore decreasing the temperature of the surroundings. This means that the enthalpy of the system increases giving a positive $\Delta H$.

Enthalpy Changes

An enthalpy change is the heat exchange with the surroundings during a chemical reaction at constant pressure. It can be calculated by doing:

$$ \Delta H = H_{\text{products}} - H_{\text{reactants}} $$

Generally, all chemical systems either release energy (exothermic reactions) or absorb energy (endothermic reaction).

Exothermic

Below are some examples of exothermic reactions:

Oxidation of fuels
In this reaction, the enthalpy of the products is less than the reactants therefore, therefor there is negative enthalpy change:

$$ CH_{4(g)} + 2O_{2(g)} \rightarrow CO_{2(g)} + 2H_{2}O_{(l)}
\hspace2ex \Delta H = -890\,kJ\,mol^{-1}
$$

Respiration
This where sugars such as glucose are oxidised to form carbon dioxide and water, producing energy.
$$ C_{6}H_{12}O_{6(aq)} + 6O_{2(g)} \rightarrow 6CO_{2(g)} + 6H_{2}O_{(l)}
\hspace2ex \Delta H = -2801\,kJ\,mol^{-1}
$$

Endothermic

Below are examples of endothermic reactions:

Thermal decomposition of limestone
Limestone containing calcium carbonate, $CaCO_{3}$ can be decomposed by heat, which uses energy to break the bonds.
$$ CaCO_{3(s)} \rightarrow CaO_{(s)} + CO_{2(g)}
\hspace2ex \Delta H = +178\,kJ\,mol^{-1}
$$
Photosynthesis
Photosynthesis is the process where sugars are produced from carbon dioxide and water.
$$ 6CO_{2(g)} + 6H_{2}O_{(l)} \rightarrow C_{6}H_{12}O_{6(aq)} + 6O_{2(g)}
\hspace2ex \Delta H = +2801\,kJ\,mol^{-1}
$$

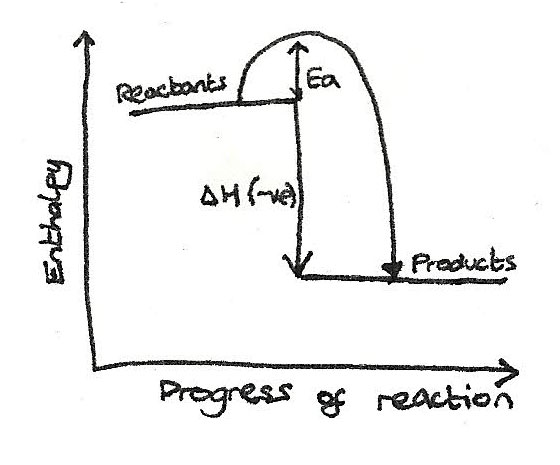
Activation Energy

This is the minimum energy required in order to start a reaction by breaking bonds in the reactants. The activation energy can be shown on energy profile diagrams.

Energy Profile Diagrams

Reactions and the enthalpy changes can be illustrated on an enthalpy profile diagram.

Exothermic Reactions
For these reactions, the enthalpy of the reactants is greater than the enthalpy of the products.
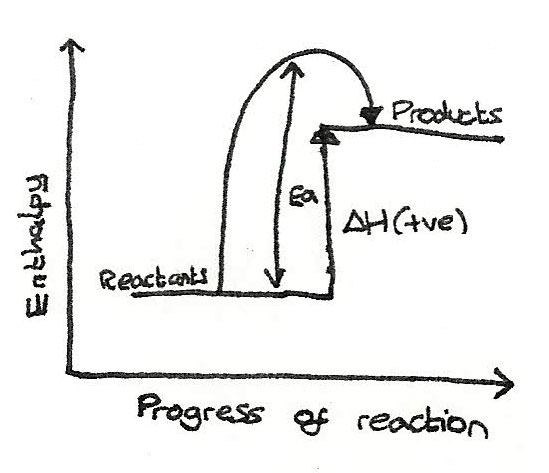
Endothermic
For these reactions, the enthalpy of the reactants is less than the enthalpy of the products.

Standard Enthalpy Changes

In order to compare and analyse reactions, values of standard enthalpy changes are made which are measured under standard conditions:

Pressure of 100 kPa (1 atmosphere)
298K (25°)
$1 mol\,dm^{-3}$ for aqueous solutions

Standard States

For a standard enthalpy change, any substance must be in its standard state. A standard state is the physical state of a substance under standard conditions.

Standard Enthalpy Change of Reaction

The standard enthalpy change of a reaction $\Delta H_{r}^{\ominus}$ is the enthalpy change for the molar quantities stated in a reaction, under standard conditions with substances in their standard states.

Standard Enthalpy Change of Combustion

The standard enthalpy change of combustion $ \Delta H_{c}^{\ominus}$ is the enthalpy change that occurs when one mole of a substance is burned in excess oxygen under standard conditions and in its standard state.

Standard Enthalpy Change of Formation

The standard enthalpy change of formation $ \Delta H_{f}^{\ominus} $ is the enthalpy change that occurs when one mole of a compound is formed from its constituent elements.

Determination of Enthalpy Changes

By measuring the temperature changes in the surroundings, the enthalpy change of the chemical system can be determined. The formula for heat exchange is:
$$ Q = mc \Delta T $$

Where $Q$ is change in energy, $m$ is the mass of the surroundings, $c$ is the specific heat capacity, and $\Delta T$ is the change in temperature.

Worked Example

$25cm^{3}$ of $2.00\,mol\,dm^{-3}\,HCl_{(aq)}$ was mixed with $25cm^{3}$ of $2.00\,mol\,dm^{-3}\,NaOH_{(aq)}$. The temperature increased from 22.5°C to 34.5°C. Find the enthalpy change of the reaction.

First the energy change must be found:
$$ \eqalign{
Q &= mc \Delta T \\
Q &= 50 \times 4.18 \times (34.5-22.5) \\
Q &= 2508J} $$
Next, the number of moles must be determined:
$$ \eqalign{
n &= c \times v \\
n &= (25 \times 10^{-3}) \times 2 \\
n &= 0.05\,mol}
$$
Now the enthalpy change can be calculated:
$$ \eqalign{
\Delta H &= \frac{Q}{n} \\
\Delta H &= \frac {-2508}{0.05} \\
\Delta H &= -50.2\,kJ\,mol^{-1}} $$

Enthalpy change of combustion

The enthalpy change of combustion is the enthalpy change when one mole of a reactant completely burns in excess oxygen. This enthalpy change can be found using a fuel and spirit burner. With this, the mass of the water and the temperature change when the fuel is burned must be recorded.

Bond Enthalpy

This is the enthalpy change that takes place when breaking one mole of a given bond in the molecules of a gaseous species by homolytic fission.

When bonds break, energy is needed so the process is endothermic.
When bonds form, energy is released so the process is exothermic.

Average Bond Enthalpies

As the strength of the bond depends on the environment it is in, average bond enthalpies can be used.

In an exothermic reaction, the bonds that are formed are stronger than the bonds that are broken. Bond making is an exothermic process.
In an endothermic reaction, the bonds that are formed are weaker than the bonds that are broken. Bond breaking is an endothermic process.

The enthalpy change of a reaction can be found with:
$$ \Delta H = \Sigma\text{(bond enthalpies broken)} - \Sigma\text{(bond enthalpies made)} $$

Hess's Law

Sometimes it can be difficult to measure the enthalpy change directly due to a high activation energy, slow reaction time or more than one reaction occurring at once forming many products.

Hess's Law allows the enthalpy change to be found indirectly. It states that if a reaction can take place by more than one route and the initial and final conditions are the same, the total enthalpy change is the same for each route.

Known Formation Enthalpies

To find the enthalpy change of combustion with known enthalpy changes of formation, the following formula can be used:

$$ \Delta H = \Sigma \Delta H_{c}\text{(products)} - \Sigma \Delta H_{c}\text{(reactants)} $$

Known Combustion Enthalpies

To find the enthalpy change of formation with known enthalpy changes of combustion, this formula can be used:

$$ \Delta H = \Sigma \Delta H_{c}\text{(reactants)} - \Sigma \Delta H_{c}\text{(products)} $$