Forces in Equilibrium
Scalar and Vectors
A vector is any physical quantity that has both direction as well as magnitude. Vectors include:
- Velocity: This is speed with a given direction.
- Displacement: This is the straight line distance from the start point, regardless of the route taken.
- Acceleration: The change in speed over time in a given direction.
A scalar is a physical quantity that only has magnitude with no direction. Scalars include:
- Speed: This is the rate at which something moves. It is always positive as it does not take into account direction.
- Density: Density is defined as the mass per unit volume. As it is calculated by dividing the mass which is a scalar by the volume which is also a scalar, density is also a scalar.
Resolving Vectors
Vectors can be added in order to calculate a resultant vector. This contains the magnitude of the combined forces and the direction the vectors are acting in total.
Straight Line
For vectors acting in a straight line, the resultant vector is the sum of the vectors in one direction subtracted with the sum of the vectors in the other direction. This will be acting in the direction with the greatest force.
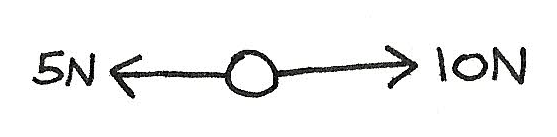
$$ R(\rightarrow) \\
\eqalign{
\text{Resultant} &= 10 - 5 \\
&= 5N\,\text{Acting}\, \rightarrow} $$
Perpendicular
For vectors acting perpendicular to each other a right angle triangle can be formed, and trigonometry can be used.
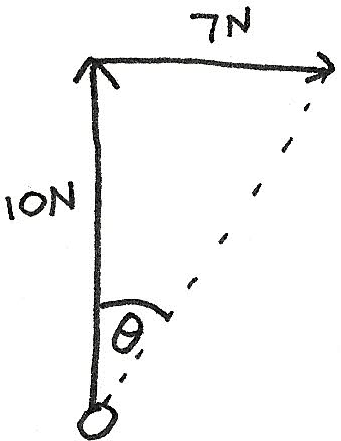
$$ \eqalign{
\text{Resultant} &= \sqrt{7^2 + 10^2} \\
&= \sqrt{149}N} \\
\eqalign{
tan\,\theta &= \frac{7}{10} \\
\theta &= 35°} $$
Components of a force
It is possible to split a force into its horizontal and vertical components. This can be done by forming a triangle, with the hypotenuse as the resultant.
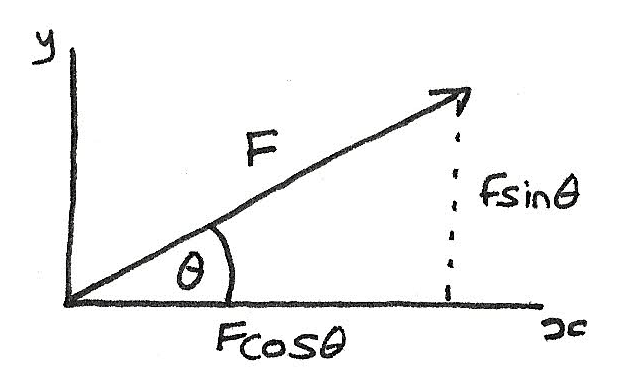
$$ R(\rightarrow) = Fcos\,\theta \\
R(\uparrow) = Fsin\,\theta $$
Balanced Forces
If two equal and opposite forces act on an object, the object is in equilibrium or constant velocity. An example of this is an object resting on a horizontal surface. The weight of the object is equal and opposite to the resistive force acting upwards.
Moments
The moment of a force around any point is defined as the force multiplied by the perpendicular distance from the line of action of the force to the point. It is measured in $Nm$.
$$ M = F \times d$$
The greater the distance, $d$, the greater the moment. If moments are taken around the point $S$, the moment will be:
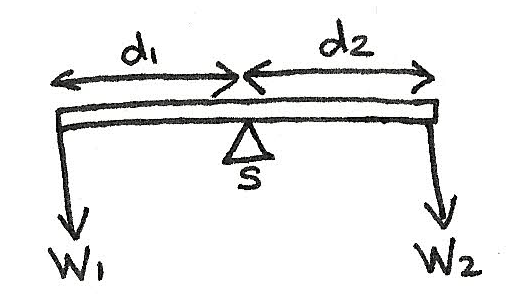
$$ \text{Moments around S} \\
d_{1}W_{1} = d_{2}W_{2} $$
If values are added:
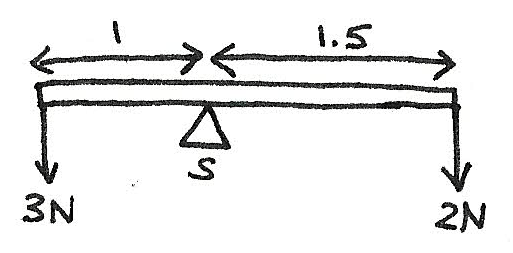
$$ \text{Moments around S} \\
\eqalign{
(1)(3) &= (1.5)(2) \\
3 &= 3} $$
As the anticlockwise moments are equal to the clockwise moments it can be seen that the system is in equilibrium.
Principle of moments
When a body is acted upon by more than one force and it remains in equilibrium, the turning effects cancel out. This is known as the principle of moments for when a body is in equilibrium, the sum of the clockwise moments acting on a point is equal to the sum of the anticlockwise moments.
Centre of mass
The centre of mass of a body is the point at which a single force on the body has no turning effect. It is the point where the weight is seen to be acting upon. The higher the centre of gravity, and the smaller the base area, the less stable the object is.
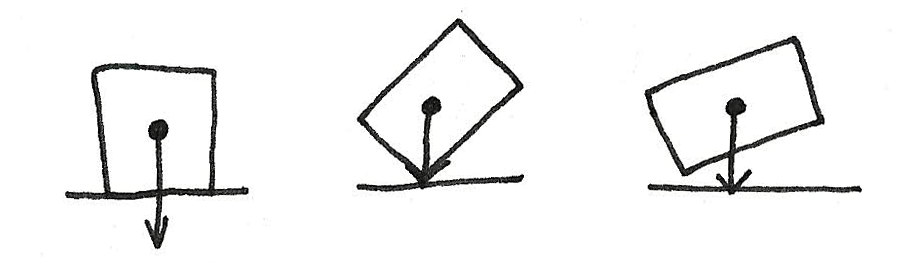
An object will fall if the vertical action of the weight sits outside of the base of the object.
Couples
A couple is a pair of equal forces acting parallel to each other in opposite directions. This produces no resultant force however a torque is produced.
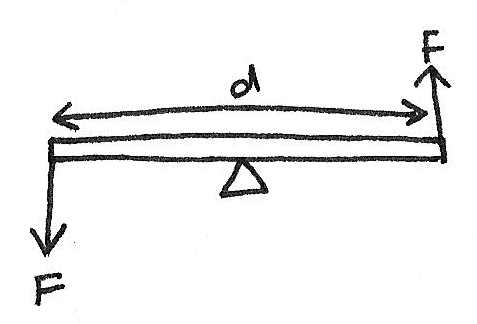
$$ T = f \times d $$
Where $T$ is the torque in $Nm$, $f$ is the size of one of the forces and $d$ is the distance between both the forces.
Equilibrium
When a system is in equilibrium, it means that the object is stationary or at constant velocity.
Stable Equilibrium
This is where when an object is moved from equilibrium, it quickly returns to the equilibrium position.
Unstable Equilibrium
This is where if an object is moved from the equilibrium position, it does not return to the equilibrium position.
For an object to be in equilibrium:
- The resultant of the forces acting on a point must be zero.
- The principle of moments must apply